题目内容
若F1、F2,为双曲线
(Ⅰ)求此双曲线的离心率;
(Ⅱ)若此双曲线过点N(2,![]() ),求双曲线方程;
),求双曲线方程;
(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1、B2(B1在y轴正半轴上),过B2作直线AB与双曲线交于A、B两点,求![]() 时,直线AB的方程.
时,直线AB的方程.
解:(Ⅰ)由![]() 知四边形PF1OM为平行四边形,
知四边形PF1OM为平行四边形,
又由
知OP平分∠F1OM,∴PF1OM为菱形,
设半焦距为c,由|![]() |=c知|
|=c知|![]() |=c,
|=c,
|![]() |=c,∴|
|=c,∴|![]() |=|
|=|![]() |+2a=c+2a,
|+2a=c+2a,
又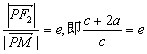
e2-e-2=0,∴e=2.(e=-1舍去)
(Ⅱ)∵e=2=![]() ,∴c=2a,
,∴c=2a,
∴双曲线方程为![]() ,将点(2,
,将点(2,![]() )代入,有
)代入,有![]() ,∴a2=3.
,∴a2=3.
即所求双曲线方程为![]() .
.
(Ⅲ)依题意得B1(0,3),B2(0,-3).
设直线AB的方程为y=kx-3,A(x1,y1),B(x2,y2).
则由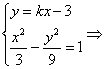 (3-k2)x2+6kx-18=0.
(3-k2)x2+6kx-18=0.
∵双曲线的渐近线为y=±![]() x,
x,
∴当k=±![]() 时,AB与双曲线只有一个交点,
时,AB与双曲线只有一个交点,
即k≠±![]() . ∵x1+x2=
. ∵x1+x2=![]() .
.
y1+y2=k(x1+x2)-6=![]() ,
,
y1y2=k2x1x2-k(x1+x2)+9=9
又![]() =(x1,y1-3),
=(x1,y1-3), ![]() =(x2,y2-3),
=(x2,y2-3),
![]() ⊥
⊥![]()
![]() x1x2+y1y2-3(y1+y2)+9=0,
x1x2+y1y2-3(y1+y2)+9=0,
∴![]() +9=0.即k2=5,∴k=±
+9=0.即k2=5,∴k=±![]() .
.
直线AB的方程为y=±![]() x-3.
x-3.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )