题目内容
已知:数列为: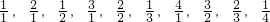 …则a2012=________.
…则a2012=________.
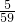
分析:将题中数列按“三角形数阵”排列,发现第一行有1个数,第二行有2个数,第三行有3个数,依此类推第k行有k个数.因此,解不等式1+2+…+k≥2012,找到满足条件的最小正整数63,说明a2012在第63行,再根据第63行第63个数得到a2012是63行第59个数,最后根据已知数列的排列规律,得到a2012的值.
解答:将题中数列按“三角形数阵”排列,得

 ,
,
 ,
, ,
,
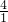 ,
, ,
, ,
,
…
由此得到第k行的排列:
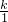 ,
,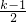 ,
,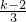 ,…,
,…, ,
, (k∈Z)
(k∈Z)假设a2012在第k行,则k是满足1+2+…+k≥2012的最小正整数
即
 ≥2012,可得满足条件的最小正整数k=63
≥2012,可得满足条件的最小正整数k=63∴a2012在第63行,并且
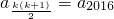 =
=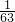 是63行的第63个数,
是63行的第63个数,因此,a2012是63行的倒数第5个,也是第59个数,可得a2012=
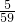
故答案为:
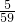
点评:本题给出一个特殊数列,要求我们发现其中规律并写出该数列的第2012项,着重考查了等差数列的通项与求和、归纳推理的一般方法等知识,属于中档题.

练习册系列答案
相关题目
 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an; (cn+
(cn+ ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.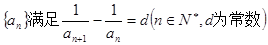 ,则称数列
,则称数列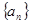 为“调和数列”.已知正项数列
为“调和数列”.已知正项数列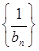 为“调和数列”,且
为“调和数列”,且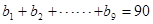 ,则
,则 的最大值是( )
的最大值是( ) 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an; (cn+
(cn+ ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.