题目内容
(2013•海口二模)正方体ABCD-A1B1C1D1的棱线长为1,面对角线B1D1上有两个动点E,F,且EF=
,则下列四个结论中①AC⊥BE ②EF∥平面ABCD ③三棱锥A-BEF的体积为定值 ④异面直线AE,BF所成的角为定值,其中正确的个数是( )
| ||
| 2 |
分析:根据线面垂直的判定与性质,可证出AC⊥BE得①正确;根据正方体的定义结合面面平行的性质,可得EF∥平面ABCD,得②正确;根据正方体的性质,可算出△BEF的面积与点A到平面BEF的距离都等于常数,从而得到三棱锥A-BEF的体积为定值,故③正确;在平面BB1D1D中作EH∥BF交B1B于H,连结AH,可得∠AEH(或其补角)等于异面直线AE、BF所成的角.观察图形的变化可得异面直线AE、BF所成的角不是定值,故④不正确.由此可得本题的答案.
解答:解: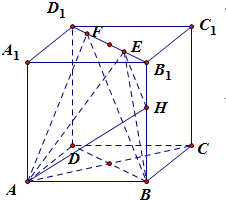 对于①,因为正方体ABCD-A1B1C1D1中,BB1⊥平面ABCD,
对于①,因为正方体ABCD-A1B1C1D1中,BB1⊥平面ABCD,
所以BB1⊥AC,结合AC⊥BD,得到AC⊥平面BB1D1D
由于BE?平面平面BB1D1D,从而得到AC⊥BE,故①正确;
对于②,因为正方体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,
且EF?平面A1B1C1D1,结合面面平行的性质可得EF∥平面ABCD,
由此可得②正确;
对于③,正方体ABCD-A1B1C1D1的对角面BB1D1D中,
△BEF的面积S=
SBB1D1D=
又∵点A到平面BEF的距离为
AC=
∴三棱锥A-BEF的体积为V=
×
×
=
(定理)
由此可得③正确;
对于④,平面BB1D1D中作EH∥BF交B1B于H,连结AH,
则∠AEH(或其补角)等于异面直线AE、BF所成的角
随着EF在B1D1上运动,△AEH的形状在不断地改变,从而得到∠AEH的大小不等于定值
因此异面直线AE、BF所成的角不为定值,故④不正确.
综上所述,正确的命题是①②③,共3个
故选:C
 对于①,因为正方体ABCD-A1B1C1D1中,BB1⊥平面ABCD,
对于①,因为正方体ABCD-A1B1C1D1中,BB1⊥平面ABCD,所以BB1⊥AC,结合AC⊥BD,得到AC⊥平面BB1D1D
由于BE?平面平面BB1D1D,从而得到AC⊥BE,故①正确;
对于②,因为正方体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,
且EF?平面A1B1C1D1,结合面面平行的性质可得EF∥平面ABCD,
由此可得②正确;
对于③,正方体ABCD-A1B1C1D1的对角面BB1D1D中,
△BEF的面积S=
| 1 |
| 4 |
| ||
| 4 |
又∵点A到平面BEF的距离为
| 1 |
| 2 |
| ||
| 2 |
∴三棱锥A-BEF的体积为V=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 12 |
由此可得③正确;
对于④,平面BB1D1D中作EH∥BF交B1B于H,连结AH,
则∠AEH(或其补角)等于异面直线AE、BF所成的角
随着EF在B1D1上运动,△AEH的形状在不断地改变,从而得到∠AEH的大小不等于定值
因此异面直线AE、BF所成的角不为定值,故④不正确.
综上所述,正确的命题是①②③,共3个
故选:C
点评:本题给出正方体中的几个命题,要求我们找出其中的真命题.着重考查了正方体的性质、线面垂直的判定与性质和面面平行的性质、三棱锥的体积公式和异面直线所成角的定义等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•海口二模)已知集合M={-1,0,1},N={0,1,2},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•海口二模)已知集合M={-1,0,1},N={0,1,2},则如图所示韦恩图中的阴影部分所表示的集合为( ) (2013•海口二模)设偶函数f(x)=Asin(ωx+?)(A>0,ω>0,0<?<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则
(2013•海口二模)设偶函数f(x)=Asin(ωx+?)(A>0,ω>0,0<?<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则