题目内容
长方体ABCD-A1B1C1D1中截去一角B1-A1BC1,则它的体积是长方体体积的分析:设出长方体的三度,求出截去一角B1-A1BC1的体积,即可确定截去一角B1-A1BC1后的体积与长方体体积的比.
解答:解:设长方体的三度为:a,b,c,则长方体的体积为:abc,截去一角B1-A1BC1的体积为:
×
abc=
abc
所以截去一角B1-A1BC1后的体积与长方体体积的比为:
故答案为:
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
所以截去一角B1-A1BC1后的体积与长方体体积的比为:
| 5 |
| 6 |
故答案为:
| 5 |
| 6 |
点评:本题考查长方体的体积,棱锥的体积,考查转化思想,灵活解决问题,是数学解题的灵魂,本题是基础题.

练习册系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
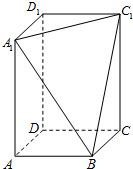 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.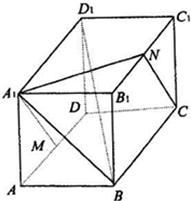 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.