题目内容
在 中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知 .
.
(1)当 ,且
,且 的面积为
的面积为 时,求a的值;
时,求a的值;
(2)当 时,求
时,求 的值.
的值.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)此题综合性较强,首先根据三角形面积公式: ,将
,将 代入得到
代入得到 与
与 的关系,根据余弦定理得到
的关系,根据余弦定理得到 与
与 的关系,再根据同角基本关系式
的关系,再根据同角基本关系式 ,列出关于
,列出关于 的关系式,得出结果;(2)由已知然后再结合余弦定理,得
的关系式,得出结果;(2)由已知然后再结合余弦定理,得 与
与 的关系,然后结合
的关系,然后结合 得出
得出 的关系,从而判定三角形的形状,由边的关系得出角的三角函数值,结合已知消
的关系,从而判定三角形的形状,由边的关系得出角的三角函数值,结合已知消 或
或 ,得出三角函数值,考察知识点比较全面,灵活转化公式之间的相互关系,进行消元.
,得出三角函数值,考察知识点比较全面,灵活转化公式之间的相互关系,进行消元.
试题解析:(1)解:因为 ,
, 的面积为
的面积为 ,
,
所以
 ,
,
所以 , 3分
, 3分
又 ,由余弦定理得
,由余弦定理得 , 5分
, 5分
由 ,所以
,所以
 ,解得
,解得 . 7分
. 7分
(2)解: ,
, ,
,
由余弦定理得, ,所以
,所以 ,
, , 9分
, 9分
由正弦定理得, , 11分
, 11分
所以
 . 13分
. 13分
考点:1.余弦定理;2.三角形面积公式;3.正弦定理;4同角基本关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是  ,且
,且 =2,
=2,
 .
. 的值.
的值. =3,求b,c的值.
=3,求b,c的值.  中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知 ,
, ,则
,则 = _______
= _______ (
( ,
, ),且函数
),且函数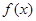 的最小正周期为
的最小正周期为 .
. 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为 ,若
,若 =1,
=1,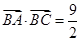 ,且
,且 ,求边长
,求边长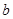 .
. 中,角A,B,C所对的边分别为a,b,c,若
中,角A,B,C所对的边分别为a,b,c,若 ,
, ,
, ,则角A的大小为
,则角A的大小为  中,角A、B、C所对的边分别为a,b,c,S表示
中,角A、B、C所对的边分别为a,b,c,S表示 =
= ( )
( )