题目内容
已知函数
，当
，
有极大值7；当
时，有极小值.
（Ⅰ）、求
，
，
的值.
（Ⅱ）、设
，求
的单调区间.
【答案】
21、（本小题满分12分）
解：（Ⅰ）、
由题意得，
，解得
，
，
（Ⅱ）、由（Ⅰ）得
于是
当
时,有
或
,
所以函数
的单调递增区间是
和
当
时,有
所以函数的单调递减区间是
【解析】略
练习册系列答案
阅读快车系列答案
相关题目
，当
时，有极大值
；
的值；（2）求函数
的极小值。
，当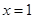
时，有极大值
。
的值；
的极小值。
，当
时，有极大值
；
的值；（2）求函数的极小值。
，当
时，有极大值
；
的值；（2）求函数
的极小值