题目内容
试证:不论正数a,b,c是等差数列还是等比数列,当n>1,n∈N且a,b,c互不相等时,都有an+cn>2bn.(n∈N).
证明 (1)设a、b、c为等比数列,a= ,c=bq(q>0且q≠1)
,c=bq(q>0且q≠1)
∴an+cn= +bnqn=bn(
+bnqn=bn(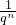 +qn)>2bn
+qn)>2bn
(2)设a、b、c为等差数列,
则2b=a+c猜想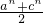 >
>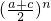 (n≥2且n∈N*)
(n≥2且n∈N*)
下面用数学归纳法证明
①当n=2时,由2(a2+c2)>(a+c)2,∴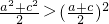
②设n=k时成立,即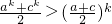 .
.
则当n=k+1时,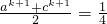 (ak+1+ck+1+ak+1+ck+1)>
(ak+1+ck+1+ak+1+ck+1)> (ak+1+ck+1+ak•c+ck•a)=
(ak+1+ck+1+ak•c+ck•a)= (ak+ck)(a+c)
(ak+ck)(a+c)
>( )k•(
)k•( )=(
)=( )k+1
)k+1
也就是说,等式对n=k+1也成立
由①②知,an+cn>2bn对一切自然数n均成立
分析:首先题目要求证明不等式对等比数列或等差数列均成立,考虑到用数学归纳法证明,本题中使用到结论有 (ak-ck)(a-c)>0恒成立(a、b、c为正数),从而ak+1+ck+1>ak•c+ck•a.即可得到答案.
点评:本题主要考查数学归纳法证明不等式,等差数列、等比数列的性质及数学归纳法证明不等式的一般步骤.属于综合性试题有一定的难度.
 ,c=bq(q>0且q≠1)
,c=bq(q>0且q≠1)∴an+cn=
 +bnqn=bn(
+bnqn=bn(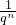 +qn)>2bn
+qn)>2bn(2)设a、b、c为等差数列,
则2b=a+c猜想
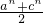 >
>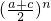 (n≥2且n∈N*)
(n≥2且n∈N*)下面用数学归纳法证明
①当n=2时,由2(a2+c2)>(a+c)2,∴
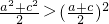
②设n=k时成立,即
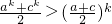 .
.则当n=k+1时,
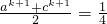 (ak+1+ck+1+ak+1+ck+1)>
(ak+1+ck+1+ak+1+ck+1)> (ak+1+ck+1+ak•c+ck•a)=
(ak+1+ck+1+ak•c+ck•a)= (ak+ck)(a+c)
(ak+ck)(a+c)>(
 )k•(
)k•( )=(
)=( )k+1
)k+1也就是说,等式对n=k+1也成立
由①②知,an+cn>2bn对一切自然数n均成立
分析:首先题目要求证明不等式对等比数列或等差数列均成立,考虑到用数学归纳法证明,本题中使用到结论有 (ak-ck)(a-c)>0恒成立(a、b、c为正数),从而ak+1+ck+1>ak•c+ck•a.即可得到答案.
点评:本题主要考查数学归纳法证明不等式,等差数列、等比数列的性质及数学归纳法证明不等式的一般步骤.属于综合性试题有一定的难度.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目