题目内容
(本小题满分14分)
如图,在四棱锥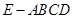 中,
中,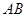 ⊥平面
⊥平面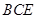 ,
,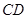 ⊥平面
⊥平面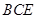 ,
,
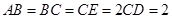 ,
,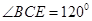 。
。
(1)求证:平面ADE⊥平面ABE;
(2)求二面角A—EB—D的余弦值.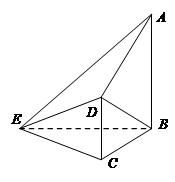
如图,在四棱锥
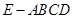 中,
中,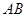 ⊥平面
⊥平面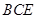 ,
,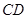 ⊥平面
⊥平面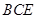 ,
,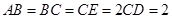 ,
,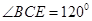 。
。(1)求证:平面ADE⊥平面ABE;
(2)求二面角A—EB—D的余弦值.
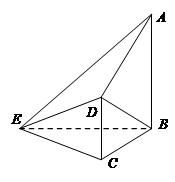
(1)见解析;(2)二面角A—EB—D的余弦值为 。
。
 。
。本试题主要是考查了立体几何中面面垂直的证明以及二面角的求解的综合运用
(1)取BE的中点O,连OC,∵BC="CE," ∴OC⊥BE,又AB⊥平面BCE. 以O为原点建立如图空间直角坐标系O-xyz,则由已知条件表示点的坐标,利用平面的法向量与法向量的夹角来得到证明。
(2)在第一问的基础上得到平面的法向量,结合向量的夹角公式得到结论。
(1)解:取BE的中点O,连OC,∵BC="CE," ∴OC⊥BE,又AB⊥平面BCE. 以O为原点建立如图空间直角坐标系O-xyz,则由已知条件有:
 ,
, ,
, ,
, ,
, ……2分
……2分
设平面ADE的法向量为 ,
,
则由

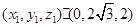

及



可取

 …………4分
…………4分
又AB⊥平面BCE,∴AB⊥OC,OC⊥平面ABE,
∴平面ABE的法向量可取为 =
= . ……6分
. ……6分
∵ ·
·

 ,∴
,∴ ⊥
⊥ ,∴平面ADE⊥平面ABE. ……8分
,∴平面ADE⊥平面ABE. ……8分
(2)设平面BDE的法向量为 ,
,
则由
及 可取
可取 …………11分
…………11分
∵平面ABE的法向量可取为 …………12分
…………12分
∴锐二面角A—EB—D的余弦值为 ,
,
∴二面角A—EB—D的余弦值为 …………14分
…………14分
(1)取BE的中点O,连OC,∵BC="CE," ∴OC⊥BE,又AB⊥平面BCE. 以O为原点建立如图空间直角坐标系O-xyz,则由已知条件表示点的坐标,利用平面的法向量与法向量的夹角来得到证明。
(2)在第一问的基础上得到平面的法向量,结合向量的夹角公式得到结论。
(1)解:取BE的中点O,连OC,∵BC="CE," ∴OC⊥BE,又AB⊥平面BCE. 以O为原点建立如图空间直角坐标系O-xyz,则由已知条件有:
 ,
, ,
, ,
, ,
, ……2分
……2分设平面ADE的法向量为
 ,
,则由


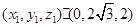

及




可取


 …………4分
…………4分又AB⊥平面BCE,∴AB⊥OC,OC⊥平面ABE,
∴平面ABE的法向量可取为
 =
= . ……6分
. ……6分∵
 ·
·

 ,∴
,∴ ⊥
⊥ ,∴平面ADE⊥平面ABE. ……8分
,∴平面ADE⊥平面ABE. ……8分(2)设平面BDE的法向量为
 ,
,则由

及
 可取
可取 …………11分
…………11分∵平面ABE的法向量可取为
 …………12分
…………12分∴锐二面角A—EB—D的余弦值为
 ,
, ∴二面角A—EB—D的余弦值为
 …………14分
…………14分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 中,
中, 底面
底面 ,四边形
,四边形 ,
, ,
,  ,
, ,E为
,E为 中点.
中点.
 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,则下列命题中正确的是( )
是一条直线,则下列命题中正确的是( )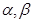 的所成角相等,则
的所成角相等,则
 ,则
,则
 的距离相等,则
的距离相等,则
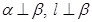 ,则
,则 中,E是棱
中,E是棱 的中点,则BE与平面
的中点,则BE与平面 所成角的正弦值为
所成角的正弦值为



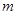 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面.考查下列命题,其中正确的命题是( )
是两个不同的平面.考查下列命题,其中正确的命题是( )



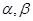 为两个不同的平面,下列四个命题中,正确的命题个数是
为两个不同的平面,下列四个命题中,正确的命题个数是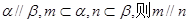 ;
;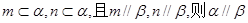
 ;
; 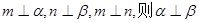
 是两个不重合的平面,
是两个不重合的平面, 是两条不同的直线,给出下列命题:
是两条不同的直线,给出下列命题: ∥
∥ ,
, ∥
∥ ∥
∥ ∥
∥ ,则
,则 ∥
∥ 则
则
 ∥
∥ ∥
∥ ,其中正确的有 (只填序号)
,其中正确的有 (只填序号) ,
, 是两个不同的平面, m,n是两条不重合的直线,下列命题中正确的是
是两个不同的平面, m,n是两条不重合的直线,下列命题中正确的是