题目内容
16.若向量$\overrightarrow a$在向量$\vec b$方向上的投影为3,且$|{\vec b}|=4$,则$\overrightarrow a•\overrightarrow b$=( )| A. | 3 | B. | 6 | C. | 12 | D. | 24 |
分析 利用向量的数量积公式得到向量的投影,列出方程求出$\overrightarrow a•\overrightarrow b$.
解答 解:向量$\overrightarrow a$在向量$\vec b$方向上的投影为3,|$\overrightarrow{a}$|cos$<\overrightarrow{a},\overrightarrow{b}>$=3且$|{\vec b}|=4$,
∴$\overrightarrow a•\overrightarrow b$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos$<\overrightarrow{a},\overrightarrow{b}>$=12
故选:C.
点评 本题考查向量的数量积的应用:求向量的投影,是基础题.

练习册系列答案
相关题目
6.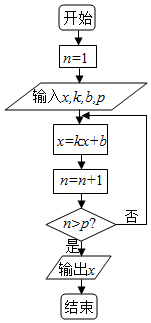 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | 19 | C. | 47 | D. | -5 |
4.已知f(x)是定义在R上的偶函数,并且满足f(x+2)=-$\frac{1}{f(x)}$,当2≤x≤3时,f(x)=x,则f(109.5)=( )
| A. | -2.5 | B. | 2.5 | C. | 5.5 | D. | -5.5 |