题目内容
如图所示,四边形ABCD是边长为2的正方形,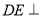 平面ABCD,AF//DE,DE=2AF,BE与平面ABCD所成角的正切值为
平面ABCD,AF//DE,DE=2AF,BE与平面ABCD所成角的正切值为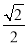 .
.
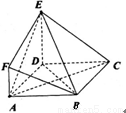
(1)求证:AC//平面EFB;
(2)求二面角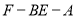 的大小.
的大小.
(1)见解析;(2)二面角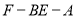 的大小为
的大小为 .
.
【解析】
试题分析:(1)设AC、BD交于O,取EB的中点G.连结FG,GO.
在△BDE中,OG∥DE且OG=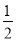 DE,FA∥DE且FA=
DE,FA∥DE且FA=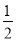 DE,∴OG∥FA且OG=FA,
DE,∴OG∥FA且OG=FA,
∴四边形FAOG为平行四边形. 2分
∴FG∥AO,又AG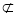 平面EFB,FG
平面EFB,FG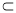 平面EFB,
平面EFB,
∴直线AC∥平面EFB; 4分
(2)∵DE⊥平面ABCD,∴BE与平面ABCD所成角就是∠DBE.
又BE与平面ABCD所成的角的正切值为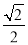 ,∴
,∴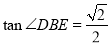 ,而BD=
,而BD=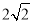 ,∴DE=2. 6分
,∴DE=2. 6分
分别以DA、DC、DE所在的直线为x,y,z轴,建立空间直角坐标系D-xyz,则有A(2,0,0),B(2,2,0),E(0,0,2),F(2,0,1),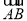 =(0,2,0),
=(0,2,0),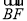 =(0,-2,1),
=(0,-2,1),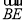 =(-2,-2,2),
=(-2,-2,2),
设平面AEB的法向量为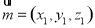 ,则
,则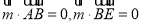 ,即
,即 ,
,
令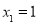 ,可得
,可得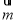 =(1,0,1), 9分
=(1,0,1), 9分
设平面FBE的法向量为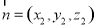 ,
, ,则
,则 ,
,
令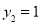 ,可得
,可得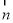 =(1,1,2), 11分
=(1,1,2), 11分
设二面角F-BE-A的大小为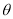 ,
,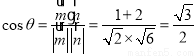 ,
,
∴二面角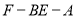 的大小为
的大小为 . 12分
. 12分
考点:考查了直线与平面平行的判定,二面角的大小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 满足约束条件
满足约束条件 若目标函数
若目标函数 的最大值为10,则
的最大值为10,则 的最小值为 .
的最小值为 . B.
B.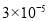 C.
C.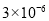 D.
D.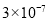
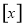 表示不超过
表示不超过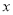 的最大整数,例如
的最大整数,例如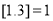 ,
,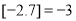 .函数
.函数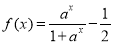
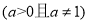 ,在
,在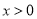 时恒有
时恒有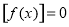 ,则实数
,则实数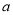 的取值范围是( )
的取值范围是( )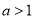 B.
B.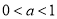 C.
C.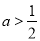 D.
D.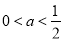
 在点
在点 处的切线方程为 .
处的切线方程为 .