题目内容
设抛物线 .
.(1)求此抛物线的方程;
(2)设直线AB上有一点Q,使得A,Q,B三点到抛物线准线的距离成等差数列,求Q点坐标;
(3)在抛物线上求一点M,使M到Q点距离与M到焦点的距离之和最小.
【答案】分析:(1)联立方程组,得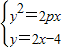 ,整理得:2x2-(8+p)x+8=0,设A(x1,y1),B(x2,y2),
,整理得:2x2-(8+p)x+8=0,设A(x1,y1),B(x2,y2),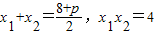 ,
,
由弦长AB= =
=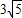 ,能导出此抛物线的方程.
,能导出此抛物线的方程.
(2)设Q(x,y),由A,Q,B三点到抛物线准线的距离成等差数列,知x=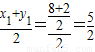 ,由此能求出Q点坐标.
,由此能求出Q点坐标.
(3)由M到Q点距离与M到焦点的距离之和最小值是Q到准线的距离,知M点的纵坐标是y=1,由此能求出点M.
解答:解:(1)联立方程组,得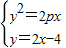 ,整理得:2x2-(8+p)x+8=0
,整理得:2x2-(8+p)x+8=0
设A(x1,y1),B(x2,y2),
则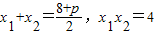 ,
,
∴弦长AB=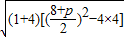 =
=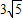 ,
,
解得p=2或-18(舍),
所以此抛物线的方程:y2=4x.
(2)设Q(x,y),
∵A,Q,B三点到抛物线准线的距离成等差数列,
∴x=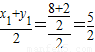 ,
,
∴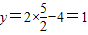 ,
,
∴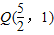 .
.
(3)∵M到Q点距离与M到焦点的距离之和最小值是Q到准线的距离,
∴M点的纵坐标是y=1,
把y=1代入y2=4x,得x= ,
,
∴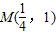 .
.
点评:本题考查抛物线方程和点的坐标的求法,解题时要认真审题,注意等差数列和抛物线性质的灵活运用.
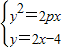 ,整理得:2x2-(8+p)x+8=0,设A(x1,y1),B(x2,y2),
,整理得:2x2-(8+p)x+8=0,设A(x1,y1),B(x2,y2),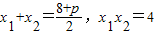 ,
,由弦长AB=
 =
=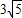 ,能导出此抛物线的方程.
,能导出此抛物线的方程.(2)设Q(x,y),由A,Q,B三点到抛物线准线的距离成等差数列,知x=
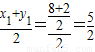 ,由此能求出Q点坐标.
,由此能求出Q点坐标.(3)由M到Q点距离与M到焦点的距离之和最小值是Q到准线的距离,知M点的纵坐标是y=1,由此能求出点M.
解答:解:(1)联立方程组,得
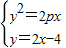 ,整理得:2x2-(8+p)x+8=0
,整理得:2x2-(8+p)x+8=0设A(x1,y1),B(x2,y2),
则
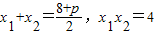 ,
,∴弦长AB=
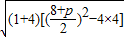 =
=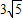 ,
,解得p=2或-18(舍),
所以此抛物线的方程:y2=4x.
(2)设Q(x,y),
∵A,Q,B三点到抛物线准线的距离成等差数列,
∴x=
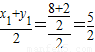 ,
,∴
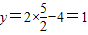 ,
,∴
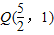 .
.(3)∵M到Q点距离与M到焦点的距离之和最小值是Q到准线的距离,
∴M点的纵坐标是y=1,
把y=1代入y2=4x,得x=
 ,
,∴
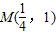 .
.点评:本题考查抛物线方程和点的坐标的求法,解题时要认真审题,注意等差数列和抛物线性质的灵活运用.

练习册系列答案
相关题目
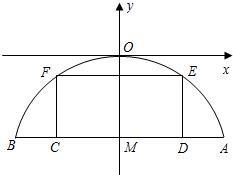 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.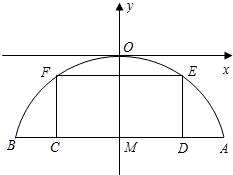 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.