题目内容
设函数![]() .
.
(I)求![]() 的表达式;
的表达式;
(Ⅱ)求函数![]() 的单调区间、极大值和极小值;
的单调区间、极大值和极小值;
(Ⅲ)若![]() 时,恒有
时,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:(I)![]() .
.
(Ⅱ)令![]() ,
,![]() .
.
则当![]() 变化时,
变化时,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| 递增 |
| 递减 | -9 | 递增 |
可知:当![]() 时,函数
时,函数![]() 为增函数.
为增函数.
当![]() 时,函数
时,函数![]() 也为增函数,
也为增函数,
当![]() 时,
时,![]() 为减函数
为减函数
![]() ;
;
![]() +1.
+1.
(Ⅲ)因为![]() 的对称轴为
的对称轴为![]() ,
,
且其图象的开口向上, 所以![]() 在区间
在区间![]() 上是增函数.
上是增函数.
则在区间![]() 上恒有
上恒有![]() 等价于
等价于![]() 的最小值大于-
的最小值大于-![]() 成立.
成立.
所以![]() .
.
解得![]() . 又
. 又![]() ,
,
则![]() 的取值范围是(0,1).
的取值范围是(0,1).

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
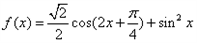 。
。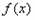 的最小正周期;
的最小正周期; 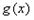 对任意
对任意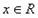 ,有
,有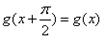 ,且当
,且当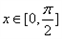 时,
时,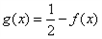 ;求函数
;求函数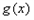 在
在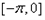 上的解析式。
上的解析式。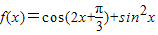 .
.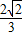 ,A为锐角,且
,A为锐角,且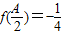 ,
,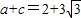 ,求△ABC的面积.
,求△ABC的面积. 与
与  共线,设函数
共线,设函数  .
. 的周期及最大值;
的周期及最大值; ,边 BC=
,边 BC= ,
, ,求
△ABC 的面积.
,求
△ABC 的面积. 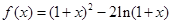 .
.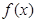 的单调区间;
的单调区间;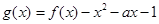 在区间
在区间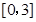 上的最小值.
上的最小值.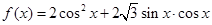 ,
, 的最小正周期以及单调增区间;
的最小正周期以及单调增区间;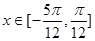 时,求
时,求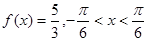 ,求
,求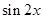 的值.
的值.