题目内容
函数f(x)=ax2+2(a-1)x+2在区间(-∞,4)上为减函数,则a的取值范围为( )
A.0<a≤ | B.0≤a≤ | C.0<a≤ | D.a> |
B
解析试题分析:根据a取值讨论是否为二次函数,然后根据二次函数的性质建立不等关系,最后将符合条件的求并集解:当a=0时,f(x)=-2x+2,符合题意,当a≠0时,要使函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数,∴a>0, ⇒0<a≤
⇒0<a≤ 综上所述0≤a≤
综上所述0≤a≤ 故选B
故选B
考点:二次函数性质
点评:本题主要考查了已知函数再某区间上的单调性求参数a的范围的问题,以及分类讨论的数学思想,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知 , 四个函数中,当
, 四个函数中,当 时, 满足不等式
时, 满足不等式 的是
的是
A. | B. |
C. | D. |
函数, 的定义域为
的定义域为
A. | B. | C. | D. |
已知函数
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时,不等式
时,不等式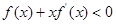 成立,若
成立,若 ,
,
 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
函数 的定义域是( )
的定义域是( )
A. | B. | C.  | D. |
下列函数中,与函数y= 定义域相同的函数为( )
定义域相同的函数为( )
A.y= | B.y= | C.y=xex | D.y= |
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 | C. 或2 或2 | D. 或1 或1 |
已知 ,则
,则 =( )
=( )
A. | B. | C. | D. |
 )的图象是( )
)的图象是( )