题目内容
函数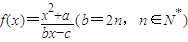 的定义域为{x|x≠1},图象过原点,且
的定义域为{x|x≠1},图象过原点,且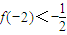 .
.(1)试求函数f(x)的单调减区间;
(2)已知各项均为负数的数列{an}前n项和为Sn,满足
 ,求证:
,求证: ;
;(3)设
 ,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由.
,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由.
【答案】分析:(1)先由己知得出a=0,b=c求得f(x)的解析式,再利用导数工具即可求出函数f(x)的单调减区间;
(2)由已知可得2Sn=an-an2,利用数列的通项与前n项和的关系式求得当数列的通项公式:an=-n,于是,待证不等式即为 .为此,我们考虑证明不等式
.为此,我们考虑证明不等式 ,下面利用导数研究函数
,下面利用导数研究函数 ,的单调性,即可证明得到
,的单调性,即可证明得到 ,即
,即 ;
;
(3)对于存在性问题,可先假设存在,只须在 中令n=1,2,3,…,20072010,并将各式相加即可得到证明.
中令n=1,2,3,…,20072010,并将各式相加即可得到证明.
解答:解:(1)由己知a=0,b=c.∵ 且b=2n,n∈N*∴b=2
且b=2n,n∈N*∴b=2
∴
于是
由f'(x)<0得0<x<1或1<x<2
故函数f(x)的单调减区间为(0,1)和(1,2)
(2)由已知可得2Sn=an-an2,
当n≥2时,2Sn-1=an-1-an-12
两式相减得(an+an-1)(an-an-1+1)=0
∴an-an-1=-1(各项均为负数)
当n=1时,2a1=a1-a12⇒a1=-1,∴an=-n
于是,待证不等式即为 .
.
为此,我们考虑证明不等式
令 ,则t>1,
,则t>1,
再令g(t)=t-1-lnt, 由t∈(1,+∞)知g'(t)>0
由t∈(1,+∞)知g'(t)>0
∴当t∈(1,+∞)时,g(t)单调递增∴g(t)>g(1)=0于是t-1>lnt
即 ①
①
令 ,
, 由t∈(1,+∞)知h'(t)>0
由t∈(1,+∞)知h'(t)>0
∴当t∈(1,+∞)时,h(t)单调递增∴h(t)>h(1)=0于是
即 ②
②
由①、②可知
所以, ,即
,即
(3)m1=2,n1=2011,m2=1,n2=2010.
在 中令n=1,2,3,…,20072010,并将各式相加得
中令n=1,2,3,…,20072010,并将各式相加得
即ln2011∈(g(2,2011),g(1,2010)).
点评:本题考查等差数列和等比数列的通项公式的求法和数列前n项和的证明,解题时要熟练掌握数列的性质和应用,注意累加法的灵活运用.
(2)由已知可得2Sn=an-an2,利用数列的通项与前n项和的关系式求得当数列的通项公式:an=-n,于是,待证不等式即为
 .为此,我们考虑证明不等式
.为此,我们考虑证明不等式 ,下面利用导数研究函数
,下面利用导数研究函数 ,的单调性,即可证明得到
,的单调性,即可证明得到 ,即
,即 ;
;(3)对于存在性问题,可先假设存在,只须在
 中令n=1,2,3,…,20072010,并将各式相加即可得到证明.
中令n=1,2,3,…,20072010,并将各式相加即可得到证明.解答:解:(1)由己知a=0,b=c.∵
 且b=2n,n∈N*∴b=2
且b=2n,n∈N*∴b=2∴

于是

由f'(x)<0得0<x<1或1<x<2
故函数f(x)的单调减区间为(0,1)和(1,2)
(2)由已知可得2Sn=an-an2,
当n≥2时,2Sn-1=an-1-an-12
两式相减得(an+an-1)(an-an-1+1)=0
∴an-an-1=-1(各项均为负数)
当n=1时,2a1=a1-a12⇒a1=-1,∴an=-n
于是,待证不等式即为
 .
.为此,我们考虑证明不等式

令
 ,则t>1,
,则t>1,
再令g(t)=t-1-lnt,
 由t∈(1,+∞)知g'(t)>0
由t∈(1,+∞)知g'(t)>0∴当t∈(1,+∞)时,g(t)单调递增∴g(t)>g(1)=0于是t-1>lnt
即
 ①
①令
 ,
, 由t∈(1,+∞)知h'(t)>0
由t∈(1,+∞)知h'(t)>0∴当t∈(1,+∞)时,h(t)单调递增∴h(t)>h(1)=0于是

即
 ②
②由①、②可知

所以,
 ,即
,即
(3)m1=2,n1=2011,m2=1,n2=2010.
在
 中令n=1,2,3,…,20072010,并将各式相加得
中令n=1,2,3,…,20072010,并将各式相加得
即ln2011∈(g(2,2011),g(1,2010)).
点评:本题考查等差数列和等比数列的通项公式的求法和数列前n项和的证明,解题时要熟练掌握数列的性质和应用,注意累加法的灵活运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 的定义域为{x|x≠1},图象过原点,且
的定义域为{x|x≠1},图象过原点,且 .
. ,求证:
,求证: .
. 的定义域为{x|x≠1},图象过原点,且
的定义域为{x|x≠1},图象过原点,且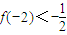 .
. ,求证:
,求证: ;
; ,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由.
,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由.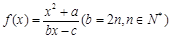 的定义域为{x| x ≠1},图象过原点,且
的定义域为{x| x ≠1},图象过原点,且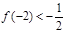 .
.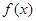 的单调减区间;
的单调减区间;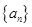 前n项和为
前n项和为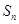 ,满足
,满足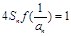 ,
,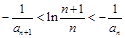 ;
;