题目内容
已函数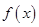 是定义在
是定义在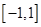 上的奇函数,在
上的奇函数,在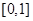 上
上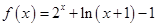 .
.
(1)求函数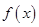 的解析式;并判断
的解析式;并判断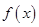 在
在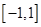 上的单调性(不要求证明);
上的单调性(不要求证明);
(2)解不等式 .
.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:{设 ,则
,则 }是求函数解析式问题的重要方法,即求那个区间的解析式设自变量在那个区间,然后运用奇函数的性质进行转化;注意运用{在相同定义域内,增
}是求函数解析式问题的重要方法,即求那个区间的解析式设自变量在那个区间,然后运用奇函数的性质进行转化;注意运用{在相同定义域内,增 增
增 增; 减
增; 减 减
减 减}判断函数的单调性.(2)利用函数的单调性解不等式,同时注意函数的定义域.
减}判断函数的单调性.(2)利用函数的单调性解不等式,同时注意函数的定义域.
试题解析:(1)
设 ,则
,则

又 是奇函数,所以
是奇函数,所以 ,
,  =
= 3分
3分

4分
 是[-1,1]上增函数
.6分
是[-1,1]上增函数
.6分
(2) 是[-1,1]上增函数,由已知得:
是[-1,1]上增函数,由已知得: .7分
.7分
等价于 ...10分
...10分

 不等式的解集为
不等式的解集为 12分
12分
考点:求函数解析式,函数的单调性,函数的奇偶性,解不等式.

练习册系列答案
相关题目
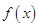 是定义在
是定义在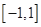 上的奇函数,在
上的奇函数,在 上时
上时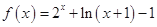
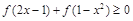 .
. 是定义在
是定义在 上的奇函数,且
上的奇函数,且 恒成立,当
恒成立,当 时,
时, 则
则 的值为(
)
的值为(
)
 B.
B.
 C.
C. D.
D. 
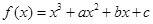 是定义在
是定义在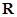 上的奇函数,其图象过点
上的奇函数,其图象过点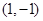 和
和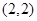 .
.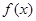 的解析式,并求
的解析式,并求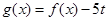 ,当实数
,当实数 如何取值时,关于
如何取值时,关于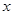 的方程
的方程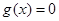 有且只有一个实
有且只有一个实 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, 。
。 的解析式;
的解析式;