题目内容
(文科)已知函数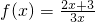 ,数列{an}满足
,数列{an}满足 .
.
(1)求数列{an}的通项公式;
(2)记Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,求Tn;
(3)令 ,若
,若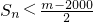 时n∈N*恒成立,求最小的正整数m.
时n∈N*恒成立,求最小的正整数m.
解:(1)由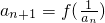 得
得 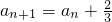
∴数列{an}为等差数列
∴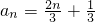 (n∈N*)
(n∈N*)
(2)Tn=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)
=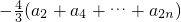
=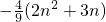
(3)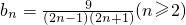 b1=3也适合上式.
b1=3也适合上式.
故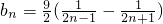
∴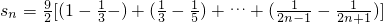 =
=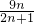
恒成立
9n2n+1<m-20002对n∈N*恒成立
又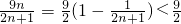
∴ ,∴m≥2009
,∴m≥2009
故最小的正整数m为2009
分析:(1)先由函数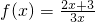 ,化简
,化简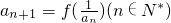 ,得
,得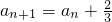 ,数列{an}为等差数列,按照等差数列通项公式来求.
,数列{an}为等差数列,按照等差数列通项公式来求.
(2)∵Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,化简得,Tn=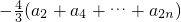 =
=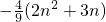 ,可用分组求和.
,可用分组求和.
(3)先根据an求bn,再用裂项求和求Sn,数列的最值问题有两种思路,一是利用数列的函数性质,二是利用数列的递推性质.
点评:本题综合考查了数列通项、数列求和、数列的函数性质,解题时要认真观察,仔细把握,灵活运用
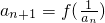 得
得 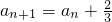
∴数列{an}为等差数列
∴
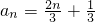 (n∈N*)
(n∈N*)(2)Tn=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)
=
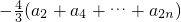
=
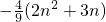
(3)
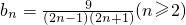 b1=3也适合上式.
b1=3也适合上式.故
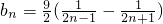
∴
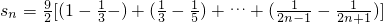 =
=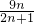
恒成立
9n2n+1<m-20002对n∈N*恒成立
又
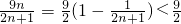
∴
 ,∴m≥2009
,∴m≥2009故最小的正整数m为2009
分析:(1)先由函数
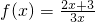 ,化简
,化简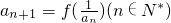 ,得
,得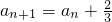 ,数列{an}为等差数列,按照等差数列通项公式来求.
,数列{an}为等差数列,按照等差数列通项公式来求.(2)∵Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,化简得,Tn=
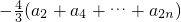 =
=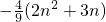 ,可用分组求和.
,可用分组求和.(3)先根据an求bn,再用裂项求和求Sn,数列的最值问题有两种思路,一是利用数列的函数性质,二是利用数列的递推性质.
点评:本题综合考查了数列通项、数列求和、数列的函数性质,解题时要认真观察,仔细把握,灵活运用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
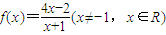 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( ) ,1) B.(
,1) B.(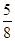 ) C.(
) C.( ) D.(
) D.(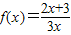 ,数列{an}满足
,数列{an}满足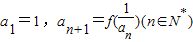 .
.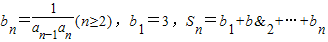 ,若
,若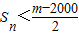 时n∈N*恒成立,求最小的正整数m.
时n∈N*恒成立,求最小的正整数m.