题目内容
(00全国卷)(本小题满分12分)
设函数![]() ,其中
,其中![]()
![]()
(I)解不等式![]() ;
;
(II)证明:当![]()
![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调函数
上是单调函数![]()
解析:(I)不等式![]() 即
即
![]() ,
,
由此得![]() ,即
,即![]() ,其中常数
,其中常数![]()
![]()
所以,原不等式等价于
![]()
即 ![]() ――3分
――3分
所以,当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() ;
;
当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]()
![]() ――6分
――6分
(II)在区间![]() 上任取
上任取![]() ,
,![]() ,使得
,使得![]() <
<![]()
![]()
![]()

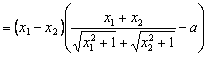
![]() ――9分
――9分
∵ ![]() ,且
,且![]() ,
,
∴ ![]() ,
,
又 ![]() ,
,
∴ ![]() ,
,
即 ![]()
![]()
所以,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调递减函数
上是单调递减函数![]() ――12分
――12分

练习册系列答案
相关题目
