题目内容
如图，一半径为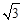
的圆形靶内有一个半径为
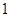的同心圆，将大圆分成两
部分，小圆内部区域记为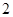
环，圆环区域记为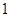环，某同学向该靶投掷
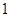枚飞镖，每次枚. 假设他每次必
定会中靶，且投中靶内各点是随机的.
（1）求该同学在一次投掷中获得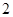环的概率；
（2）设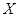
表示该同学在次投掷中获得的环数，求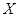的分布列及数学期望.
（1）
；（2）详见解析.
解析试题分析：（1）先根据题中条件确定相应的事件为几何概型，然后利用几何概型的概率计算公式（对应区域面积之比）求出相应事情的概率即可；（2）
（1）由题意可得是几何概型，设
，
该同学一次投掷投中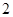环的概率为；
（2）由题意可知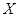可能的值为、
、
、
，
，
，
，
，
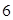的分布列为
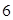
环，
答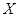：的数学期望为环.
考点：1.几何概型；2.离散型随机变量分布列与数学期望
练习册系列答案
相关题目
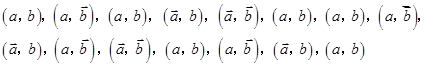
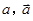分别表示甲组研发成功和失败；
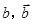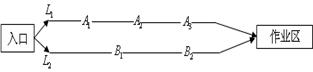
分别表示乙组研发成功和失败.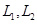
两条巷道通往作业区(如下图)，
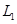巷道有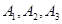
三个易堵塞点，各点被堵塞的概率都是
；
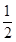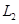巷道有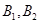
两个易堵塞点，被堵塞的概率分别为
．
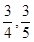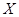，求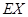
，并按照＂平均堵塞点少的巷道是较好的抢险路线＂的标准，请你帮助救援队选择一条抢险路线，并说明理由．
棵，梧桐树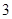
棵.它们移栽后的成活率分别
、
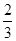，每棵树是否存活互不影响，在移栽的
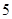棵树中：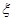
的分布列与期望.
现不放回从袋中摸取球，每次摸一球，直到取到白球时即终止，每个球在每一次被取出的机会是等可能的，用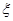
表示取球终止时所需要的取球次数.
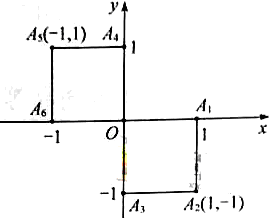
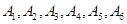（如图）这六个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为
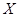，若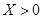
就去打球，若
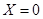就去唱歌，若
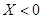就去下棋。