题目内容
求证：
．
证明：设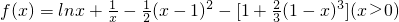 
，
则：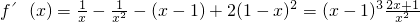
，
令f'（x）=0解得：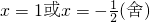
，
当x变化时，f'（x），f（x）的变化情况如下表：
∴当x=1时，函数f（x）取得极小值f（1）=0，也是唯一极小值，
∴f（x）的最小值为f（1）=0，即：f（x）≥f（1）=0，
所以．
分析：设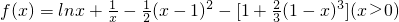，求出它的导数f'（x），根据导数的符号判断函数的单调性，进而求得函数的最小值，从而证得不等式成立．
点评：本题考查利用函数的最小值证明不等式的方法，函数的导数与函数的单调性的关系，求出f（x）的最小值是解题的关键．
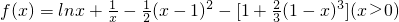，则：
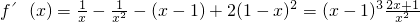，令f'（x）=0解得：
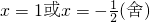，当x变化时，f'（x），f（x）的变化情况如下表：
| x | （0，1） | 1 | （1，+∞） |
| f′（x） | - | 0 | + |
| f（x） | 减函数 | 极小值 | 增函数 |
∴f（x）的最小值为f（1）=0，即：f（x）≥f（1）=0，
所以
．分析：设
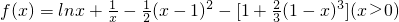，求出它的导数f'（x），根据导数的符号判断函数的单调性，进而求得函数的最小值，从而证得不等式成立．点评：本题考查利用函数的最小值证明不等式的方法，函数的导数与函数的单调性的关系，求出f（x）的最小值是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目