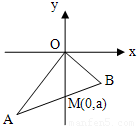
题目内容
如图，线段AB过y轴上一点N(0，m)，AB所在直线的斜率为k(k≠0)，两端点A、B到y轴的距离之差为4k.
(Ⅰ)求出以y轴为对称轴，过A、O、B三点的抛物线方程；
(Ⅱ)过抛物线的焦点F作动弦CD，过C、D两点分别作抛物线的切线，设其交点为M，求点M的轨迹方程，并求出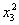
的值.
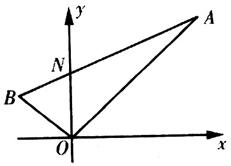
解：(Ⅰ)设AB所在直线方程为y=kx+m，抛物线方程为x2=2py，且A(x1，y1)，B(x2，y2)，
不妨设x1＞0，x2＜0 ．∴|x1|-|x2|=4k 即x1+x2=4k把y=kx+m代入x2=2py得x2-2pkx-2pm=0
∴x1+x2=2pk ∴2pk=4k ∴p=2故所求抛物线方程为x2=4y
(Ⅱ)设C(x3，
)，D(x4，
)
过抛物线上C、D两点的切线方程分别是y=
，y=
∴两条切线的交点M的坐标为(
)
设CD的直线方程为y=nx+1，代入x2=4y得x2-4nx-4=0
∴x3x4=-4 故M的坐标为(
，-1)
故点M的轨迹为y=-1.
∵
=(x3，
) 
=(x4，
)
∴
·
=x3x4+
·
-
(
)+1=x3x4+1-
(
)+1=-
(
)-2
而
+(-1-1)2=
故
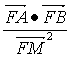=-1
练习册系列答案
相关题目
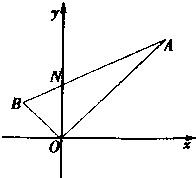如图，线段AB过y轴上一点N（0，m），AB所在直线的斜率为k（k≠0），两端点A，B到y轴的距离之差为4k．
（2007•揭阳二模）如图，线段AB过y轴负半轴上一点M（0，a），A、B两点到y轴距离的差为2k．
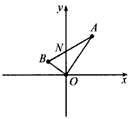
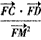的值。