题目内容
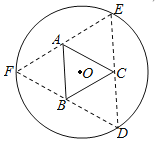
【题目】如图，圆形纸片的圆心为
，半径为
，该纸片上的等边三角形
的中心为.
，
，
为圆上的点，
分别是以
为底边的等腰三角形.沿虚线剪开后，分别以为折痕折起，使得，，重合，得到三棱锥.当所得三棱锥体积（单位：
）最大时，
的边长为_________（
）.
【答案】
【解析】
连接
，交
于点
，设
，求出
，
，构造函数，利用导数研究函数的单调性，从而得出
时，所得三棱锥体积最大时，进而得解.
如图，连接，交于点，连接
，
由题意，知
，
，
，
所以，
，所以
，
设，则，
，
三棱锥的高
，
，
则三棱锥的体积
，
令
，
则
，
令
，即
，解得，
所以，当
时，
，
在
上单调递增；
当
时，
，在
上单调递减，
所以，当时，取得极大值，也是最大值，
此时，
，
所以，当所得三棱锥体积最大时，
的边长为.
故答案为：.
练习册系列答案
优等生题库系列答案
相关题目
