Question

【题目】已知椭圆1()的离心率为，且经过点，直线与椭圆E交于B，C两点（B，C不与A重合）.

（1）求椭圆E的方程；

（2）若O，B，C三点不共线时（O为坐标原点），求面积的最大值；

（3）设直线AB，AC与轴的交点分别为P，Q，求证：.

Answer 1

【答案】（1）；（2）；（3）证明见解析.

【解析】

（1）结合待定系数法和离心率公式及椭圆的关系式联立解方程即可求解；

（2）联立直线与椭圆标准方程，由韦达定理得x1+x2=﹣m，，表示出弦长，由点到直线距离公式求得O到直线BC的距离d，结合面积公式化简可得S△OBC，由不等式性质可求最值；

（3）画出图像，需将结论进行转化，要求，即求∠AQP=∠APQ，即证kAP+kAQ=0，即证kAB+kAC=0，结合（2）化简即可得证；

（1）由题意可知:，解得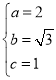，∴椭圆E的方程为：；

（2）由A不在l上，可知m≠1，由，得：x2+mx+m2﹣3=0，

∴△=m2﹣4(m2﹣3)=12﹣3m2>0，即﹣2<m<2，且m≠1，m≠0，设B(x1，y1)，C(x2，y2)，

∴x1+x2=﹣m，，

∴|BC|，

又∵点O到直线BC的距离d，

∴S△OBC，

当且仅当m（满足△>0且m≠0，1）时，△OBC的面积取得最大值；

（3）

由（2）可知x1+x2=﹣m，，∴kAP+kAQ=kAB+kAC1

10，∴∠AQP=∠APQ，∴|AP|=|AQ|.