题目内容
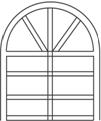
 如图,一个铝合金窗分为上、下两栏,四周框架和中间隔栏的材料为铝合金,宽均为6cm,上栏和下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800cm2,设该铝合金窗的宽和高分别为a(cm),b(cm),铝合金的透光部分的面积为S(cm2).
如图,一个铝合金窗分为上、下两栏,四周框架和中间隔栏的材料为铝合金,宽均为6cm,上栏和下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800cm2,设该铝合金窗的宽和高分别为a(cm),b(cm),铝合金的透光部分的面积为S(cm2).(1)试用a,b表示S;
(2)若要使S最大,则铝合金窗的宽和高分别为多少?
分析:(1)先根据题意分别求出上、下两栏的高和宽,然后利用矩形的面积公式将三个透光部分的面积求出相加即可得到所求;
(2)抓住ab=28800进行化简变形,然后利用基本不等式进行求解,注意等号成立的条件,最后求出取等号时a与b的值即可.
(2)抓住ab=28800进行化简变形,然后利用基本不等式进行求解,注意等号成立的条件,最后求出取等号时a与b的值即可.
解答:解:(1)根据题意可知上栏的高为
cm,长为(a-12)cm.
下栏的高为
cm,宽为
cm.
∴铝合金的透光部分的面积为S=
(a-12)+
×
×2=(b-18)(a-16)
(2)∵ab=28800
∴S=(b-18)(a-16)=29088-2(9a+8b)≤29088-4
=29088-1440×4=23328
当且仅当9a=8b时,而ab=28800
解得a=160,b=180时不等式取等号
∴若要使S最大,则铝合金窗的宽和高分别为160cm,180cm.
| b-18 |
| 3 |
下栏的高为
| 2(b-18) |
| 3 |
| a-18 |
| 2 |
∴铝合金的透光部分的面积为S=
| b-18 |
| 3 |
| 2(b-18) |
| 3 |
| a-18 |
| 2 |
(2)∵ab=28800
∴S=(b-18)(a-16)=29088-2(9a+8b)≤29088-4
| 72ab |
当且仅当9a=8b时,而ab=28800
解得a=160,b=180时不等式取等号
∴若要使S最大,则铝合金窗的宽和高分别为160cm,180cm.
点评:本题考查将实际问题转化为数学问题的能力,同时考查利用基本不等式求函数的最值注意满足的条件:一正、二定、三相等,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 是其秒针的转动中心,
是其秒针的转动中心, 是秒针的另一端,
是秒针的另一端, ,
, 是过点
是过点 在秒针
在秒针 上爬行,蚂蚁
上爬行,蚂蚁 分钟的时间内,蚂蚁
分钟的时间内,蚂蚁 .
.