题目内容
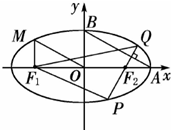
如图所示，设椭圆
的左、右焦点为
，点
分别是椭圆在
轴上的两顶点，
.
（1）求椭圆的方程；
（2）过
的直线交椭圆于
两点，在右准线
上的射影分别为
，求证：
与
的公共点在
轴上。
解：（1）由
得
，
又
得
椭圆的方程为
（2）当
不存在时，求得
与
的公共点为
在
轴上
当存在时，设
与椭圆方程联立得：
由韦达定理得：
设
同理
联立得：
即
将
代入方程中得
综上，与的公共点在轴上。
练习册系列答案
相关题目
（普通班）如图所示，从椭圆
上一点M向
轴作垂线，恰好通过椭圆的左焦点
，且它的长轴端点A及短轴端点B的连线
.
是右焦点，
的取值范围;
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图。若抛物线C2：
与y轴的交点为B，且经过F1，F2点
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
面积的最大值。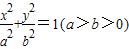
上一点M向x轴作垂线，恰好通过椭