题目内容
已知
为圆
的两条互相垂直的弦，且垂足为
，则四边形
面积的最大值为（ ）
| A．5 | B．10 | C．15 | D．20 |
A.
解析试题分析：如图，作
于
，
于
，则
，
∴
，又∵
，
∴
，当且仅当
时，等号成立，∴四边形
面积的最大值为
.
考点：1.直线与圆动态问题；2.基本不等式求最值.
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
．已知直线
：
，若以点
为圆心的圆与直线相切于点
，且在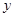
轴上，则该圆的方程为 （ ）
A． | B． |
C． | D． |
直线x=2被圆
所截弦长等于
,则a的值为 ( )
| A．-1或-3 | B． 或 | C．1或3 | D． |
方程x2+y2+2x-4y-6=0表示的图形是( )
A．以(1，-2)为圆心， 为半径的圆 |
| B．以(1，2)为圆心，为半径的圆 |
| C．以(-1，-2)为圆心，为半径的圆 |
| D．以(-1，2)为圆心，为半径的圆 |
已知O为坐标原点，直线
与圆
分别交于A,B两点．若
，则实数
的值为（ ）．
| A．1 | B． | C． | D． |
在点
处的切线为
，则直线
上的任意点Q之间的最近距离是（ ）
的一条内角平分线，点A（1，2），B（-1，-1），
求
的面积。直线tx＋y－t＋1＝0(t∈R)与圆x2＋y2－2x＋4y－4＝0的位置关系为( )
| A．相交 | B．相切 | C．相离 | D．以上都有可能 |
方程|x|－1＝
所表示的曲线是( )
| A．一个圆 | B．两个圆 | C．半个圆 | D．两个半圆 |