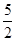题目内容
已知数列 的前n项和为
的前n项和为 ,
,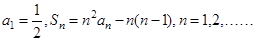
(1)证明:数列 是等差数列,并求
是等差数列,并求 ;
;
(2)设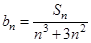 ,求证:
,求证: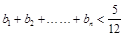 .
.
 的前n项和为
的前n项和为 ,
,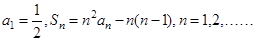
(1)证明:数列
 是等差数列,并求
是等差数列,并求 ;
;(2)设
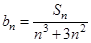 ,求证:
,求证: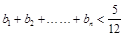 .
.(1)略 (2)



本试题主要是考查了数列的通项公式与前n项和的关系式的运用。以及运用求和得到不等式的证明。
(1)由 知,当
知,当 时:将第n项变为前n项的和的关系式,化简变形
时:将第n项变为前n项的和的关系式,化简变形 ,即得到
,即得到 ,
,
分析得证。
(2)因为由1知,∴

∴
=
得到前n项和的结论,放缩法得到结论。
(1)由
 知,当
知,当 时:将第n项变为前n项的和的关系式,化简变形
时:将第n项变为前n项的和的关系式,化简变形 ,即得到
,即得到 ,
,分析得证。
(2)因为由1知,∴


∴

=

得到前n项和的结论,放缩法得到结论。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 满足a1=0,a2=2,且对任意m,
满足a1=0,a2=2,且对任意m,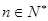 都有
都有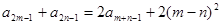
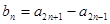
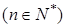 ,证明:
,证明: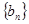 是等差数列;
是等差数列;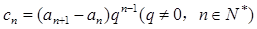 ,求数列
,求数列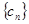 的前n项和Sn。
的前n项和Sn。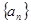 是等差数列,数列
是等差数列,数列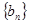 的前n项和
的前n项和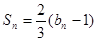 ,若
,若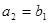 ,
,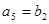 ,(1)求数列
,(1)求数列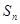 .
.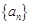 是各项均为正数的等差数列.
是各项均为正数的等差数列.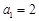 ,且
,且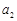 ,
,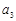 ,
,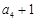 成等比数列,求数列
成等比数列,求数列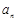 ;
;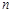 和为
和为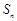 ,设
,设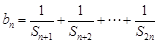 ,若对任意的
,若对任意的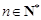 ,不等式
,不等式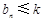 恒成立,求实数
恒成立,求实数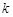 的最小值;
的最小值;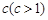 的不同次幂,求证:数列
的不同次幂,求证:数列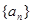 为等差数列,公差为
为等差数列,公差为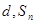 为其前
为其前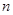 项和,
项和,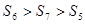 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )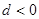
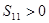
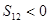
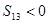
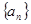 是等差数列,
是等差数列,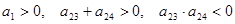 ,则使前
,则使前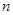 项和
项和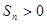 成立的最大正数
成立的最大正数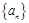 的公差不为零,
的公差不为零,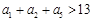 ,且
,且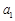 、
、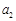 、
、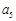 成等比数
成等比数 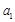 的取值范围为 .
的取值范围为 .