Question

如图，在正方体ABCD-A₁B₁C₁D₁中，M、N、P分别为棱AB、BC、DD₁的中点．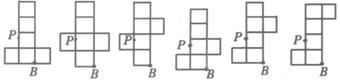

(Ⅰ)求二面角B₁-MN-B的正切值；

(Ⅱ)证明：PB⊥平面B₁MN；

(Ⅲ)画出该正方体表面展开图，使其满足“有4个正方形相连成一个长方形”的条件．

Answer 1

(Ⅰ)连结BD交MN于F,则BF⊥MN,连结B₁F.

∵B₁B⊥平面ABCD,∴B₁F⊥MN.

∴∠B₁FB为二面角B₁-MN-B的平面角. 

在Rt△B₁BF中,B₁B=1,BF=,则tan∠B₁FB=. 

(Ⅱ)过点P作PE⊥AA₁于E,则PE⊥平面ABB₁A₁,连结BE.由平面几何知识知,B₁M⊥BE. 

∴PB⊥B₁M  同理,PB⊥B₁N

故  PB⊥平面B₁MN. 

(Ⅲ)符合条件的正方体表面展开图可以是以下6种情况之一.