题目内容
已知函数
(1)当x∈R时,求f(x)的最小值;
(2)若
 ,求f(x)的单调区间.
,求f(x)的单调区间.
【答案】分析:(1)利用二倍角的余弦公式将三角函数中平方降幂,再利用二倍角的正弦公式及公式
化简三角函数为y=Asin(ωx+φ)+k形式,利用三角函数的有界性求出最小值.
(2)求出 范围,利用整体代换的思想,令
范围,利用整体代换的思想,令 在单减区间上,求出x的范围即为单调递减区间.
在单减区间上,求出x的范围即为单调递减区间.
解答:解:(1) =
=
=
当x∈R时,f(x)的最小值为3 -4.
-4.
(2)∵ ∴
∴ ,
,
∴
∴ 时,f(x)单调减区间为
时,f(x)单调减区间为 .
.
点评:本题考查三角函数的二倍角公式将三角函数的平方降幂、利用公式 化简三角函数、利用整体代换的思想求单调区间.
化简三角函数、利用整体代换的思想求单调区间.

化简三角函数为y=Asin(ωx+φ)+k形式,利用三角函数的有界性求出最小值.
(2)求出
 范围,利用整体代换的思想,令
范围,利用整体代换的思想,令 在单减区间上,求出x的范围即为单调递减区间.
在单减区间上,求出x的范围即为单调递减区间.解答:解:(1)
 =
=
=

当x∈R时,f(x)的最小值为3
 -4.
-4.(2)∵
 ∴
∴ ,
,∴

∴
 时,f(x)单调减区间为
时,f(x)单调减区间为 .
.点评:本题考查三角函数的二倍角公式将三角函数的平方降幂、利用公式
 化简三角函数、利用整体代换的思想求单调区间.
化简三角函数、利用整体代换的思想求单调区间. 
练习册系列答案
相关题目

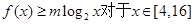 恒成立,求m的取值范围
恒成立,求m的取值范围
 恒成立,求m的取值范围.
恒成立,求m的取值范围.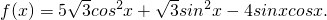
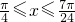 ,求f(x)的单调区间.
,求f(x)的单调区间.
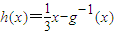 在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;
在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;