题目内容

如图，在正方体ABCD—A1B1C1D1中，E、F分别是BB1、D1B1的中点.求证：EF⊥平面B1AC.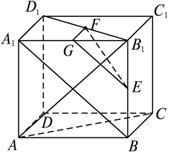

 

证明：设,,,则

       .

∴

=(b2-a2+ca+cb)

=(|b2|-|a|2+0+0)=0.

∴,即EF⊥AB1.同理EF⊥B1C.

又AB1∩B1C=B1,∴EF⊥平面B1AC.

启示：选基底，利用向量的计算来证明.

练习册系列答案
相关题目
精英家教网若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
1
h2
=
1
a2
+
1
b2
，如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记M=
1
PO2
，N=
1
PA2
+
1
PB2
+
1
PC2
，那么M、N的大小关系是
 
．
精英家教网如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记M=
1
PO2
，N=
1
PA2
+
1
PB2
+
1
PC2
，那么M，N的大小关系是
 
．
精英家教网若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
1
h2
=
1
a2
+
1
b2
，如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，类比平面几何中的结论，得到此三棱锥中的一个正确结论为
 
．
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，
（1）求证：AC⊥平面D1DB；
（2）BD1∥平面ABC．
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的主视图与左视图的面积的比值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网