题目内容
设a、b∈R,试比较a2(a+1)+b2(b+1)与a(a2+b)+b(b2+a)的大小.
思路点拨:对于要比较两个代数式的值的大小的问题,通常情况下可以考虑它们的差与零的大小关系,然后结合具体问题采用恰当的变形方式,从而说明差的符号,进而确定其大小关系.
解:因为a2(a+1)+b2(b+1)-[a(a2+b)+b(b2+a)]=a2+b2-2ab=(a-b)2≥0,
所以a2(a+1)+b2(b+1)≥a(a2+b)+b(b2+a).

练习册系列答案
相关题目
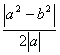 与
与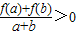 .
.