题目内容
如图,ABCD是梯形,AB∥CD,且AB=2CD,M、N分别是DC和AB的中点,已知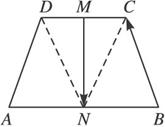
思路分析:本题要求用a、b表示![]() 和
和![]() ,而a、b不共线,由平面向量基本定理,此平面内任何向量都可用a、b唯一表示.因此需结合图形寻找
,而a、b不共线,由平面向量基本定理,此平面内任何向量都可用a、b唯一表示.因此需结合图形寻找![]() 、
、![]() 与a、b的关系.
与a、b的关系.
解:连结DN、CN,
∵N为AB的中点,而![]() =a,
=a,
∴![]() =
=![]() a.又AB=2CD,且AB∥CD,
a.又AB=2CD,且AB∥CD,
∴![]() =
=![]() a.
a.
从而![]() =
=![]() =
=![]() a.
a.
从而在△ADN中,DN=![]() -
-![]() =
=![]() a-b.
a-b.
在△DMN中,![]() =DN-
=DN-![]() =
=![]() a-b-
a-b-![]() a=
a=![]() a-b.
a-b.
在△MNC中,![]() =
=![]() -
-![]() =
=![]() a-
a-![]() a+b=b.
a+b=b.
在△NBC中,![]() =
=![]() -
-![]() =b-
=b-![]() a.
a.
∴![]() =-
=-![]() a+b,
a+b, ![]() =
=![]() a-b.
a-b.
思想方法小结:正确理解向量加减法的几何意义是解决本题的关键.应熟记![]() =
=![]() -
-![]() ,
,![]() =
=![]() +
+![]() 等结论.
等结论.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
(本小题满分14分)
|
|
 ,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点
,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点(Ⅰ)求证:AE//面PBC.
|
(本小题满分14分)
|
|
 ,PA⊥面ABCD,
,PA⊥面ABCD,
且AB=1,AD=1,CD=2,PA=3,E为PD的中点
(Ⅰ)求证:AE//面PBC.
|
|
(Ⅲ)在面PAB内能否找一点N,使NE⊥面PAC. 若存在,找出并证明;若不存在,
请说明理由。
(本小题满分14分)
|
|
 ,PA⊥面ABCD,
,PA⊥面ABCD,
且AB=1,AD=1,CD=2,PA=3,E为PD的中点
(Ⅰ)求证:AE//面PBC.
|
|
(Ⅲ)在面PAB内能否找一点N,使NE⊥面PAC. 若存在,找出并证明;若不存在,请说明理由。
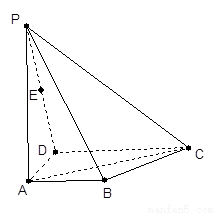
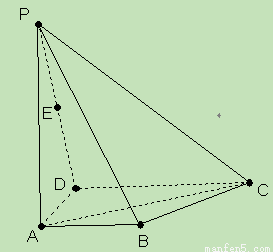
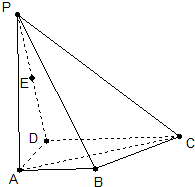 如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点
如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点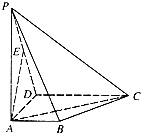 (2013•眉山一模)如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点.
(2013•眉山一模)如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点.