题目内容
有A、B、C三个盒子,每个盒子中放有红、黄、蓝颜色的球各一个,所有的球仅有颜色上的区别.
(Ⅰ)从每个盒子中任意取出一个球,记事件S为“取得红色的三个球”,事件T为“取得颜色互不相同的三个球”,求P(S)和P(T);
(Ⅱ)先从A盒中任取一球放入B盒,再从B盒中任取一球放入C盒,最后从C盒中任取一球放入A盒,设此时A盒中红球的个数为ξ,求ξ的分布列与数学期望Eξ.
(Ⅰ)从每个盒子中任意取出一个球,记事件S为“取得红色的三个球”,事件T为“取得颜色互不相同的三个球”,求P(S)和P(T);
(Ⅱ)先从A盒中任取一球放入B盒,再从B盒中任取一球放入C盒,最后从C盒中任取一球放入A盒,设此时A盒中红球的个数为ξ,求ξ的分布列与数学期望Eξ.
(Ⅰ)∵A、B、C三个盒子,
每个盒子中放有红、黄、蓝颜色的球各一个,
所有的球仅有颜色上的区别.
从每个盒子中任意取出一个球,记事件S为“取得红色的三个球”,
事件T为“取得颜色互不相同的三个球”,
∴P(S)=
×
×
=
,
P(T)=
=
.
(Ⅱ)ξ的可能值为0,1,2.
①考虑ξ=0的情形,首先A盒中必须取一个红球放入B盒,相应概率为
,
此时B盒中有2红2非红;
若从B盒中取一红球放入C盒,相应概率为
,则C盒中有2红2非红,
从C盒中只能取一个非红球放入A盒,相应概率为
;
若从B盒中取一非红球放入C盒,相应概率为
,
则C盒中有1红3非红,从C盒中只能取一个非红球放入A盒,相应概率为
.
故P(ξ=0)=
×[
×
+
×
]=
.
②考虑ξ=2的情形,首先A盒中必须取一个非红球放入B盒,相应概率为
,
此时B盒中有1红3非红;
若从B盒中取一红球放入C盒,相应概率为
,
则C盒中有2红2非红,从C盒中只能取一个红球放入A盒,相应概率为
;
若从B盒中取一非红球放入C盒,相应概率为
,
则C盒中有1红3非红,从C盒中只能取一个红球放入A盒,相应概率为
.
故P(ξ=2)=
×[
×
+
×
]=
.
③P(ξ=1)=1-
-
=
.
所以ξ的分布列为
ξ的数学期望Eξ=0×
+1×
+2×
=1.
每个盒子中放有红、黄、蓝颜色的球各一个,
所有的球仅有颜色上的区别.
从每个盒子中任意取出一个球,记事件S为“取得红色的三个球”,
事件T为“取得颜色互不相同的三个球”,
∴P(S)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
P(T)=
| ||||||
|
| 2 |
| 9 |
(Ⅱ)ξ的可能值为0,1,2.
①考虑ξ=0的情形,首先A盒中必须取一个红球放入B盒,相应概率为
| 1 |
| 3 |
此时B盒中有2红2非红;
若从B盒中取一红球放入C盒,相应概率为
| 1 |
| 2 |
从C盒中只能取一个非红球放入A盒,相应概率为
| 1 |
| 2 |
若从B盒中取一非红球放入C盒,相应概率为
| 1 |
| 2 |
则C盒中有1红3非红,从C盒中只能取一个非红球放入A盒,相应概率为
| 3 |
| 4 |
故P(ξ=0)=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 24 |
②考虑ξ=2的情形,首先A盒中必须取一个非红球放入B盒,相应概率为
| 2 |
| 3 |
此时B盒中有1红3非红;
若从B盒中取一红球放入C盒,相应概率为
| 1 |
| 4 |
则C盒中有2红2非红,从C盒中只能取一个红球放入A盒,相应概率为
| 1 |
| 2 |
若从B盒中取一非红球放入C盒,相应概率为
| 3 |
| 4 |
则C盒中有1红3非红,从C盒中只能取一个红球放入A盒,相应概率为
| 1 |
| 4 |
故P(ξ=2)=
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 5 |
| 24 |
③P(ξ=1)=1-
| 5 |
| 24 |
| 5 |
| 24 |
| 7 |
| 12 |
所以ξ的分布列为
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 5 |
| 24 |
| 7 |
| 12 |
| 5 |
| 24 |

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

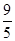 ,判断框内“
,判断框内“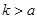 ”,且
”,且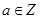 ,则
,则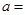 ___________.
___________.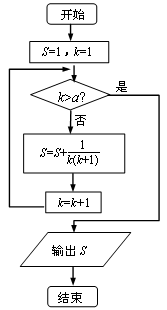
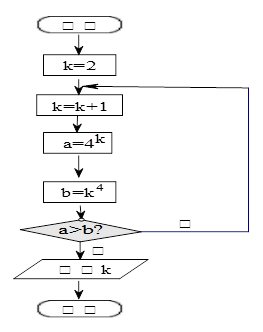
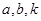 分别为1,2,3,则输出的M=( )
分别为1,2,3,则输出的M=( )