题目内容
在某电视台举办的《上海世博会知识有奖问答比赛》中,甲、乙、丙三人同时回答一道问题,已知甲回答对这道题的概率是
,甲、丙两人都回答错的概率是
,乙、丙两人都回答对的概率是
,且三人答对这道题的概率互不影响.
(Ⅰ)求乙、丙两人各自回答对这道题的概率;
(Ⅱ)求答对该题的人数ξ的分布列和数学期望Eξ.
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
(Ⅰ)求乙、丙两人各自回答对这道题的概率;
(Ⅱ)求答对该题的人数ξ的分布列和数学期望Eξ.
(Ⅰ)∵甲回答对这道题的概率是
,甲、丙两人都回答错的概率是
,
乙、丙两人都回答对的概率是
,三人答对这道题的概率互不影响.
记“甲回答对这道题”、“乙回答对这道题”、
“丙回答对这道题”分别为事件A、B、C,
则P(A)=
,
且有
即
∴P(B)=
,P(C)=
(Ⅱ)答对该题的人数ξ,ξ的可能取值:0,1,2,3,
根据相互独立事件的概率公式得到
P(ξ=0)=P(
•
•
)=
P(ξ=1)=P(A•
•
+
•
•
+
•
•C)=
P(ξ=2)=P(A•B•
+A•
•C+
•B•C)=
P(ξ=3)=P(A•B•C)=
∴ξ的分布列是

∴Eξ=1×
+2×
+3×
=
.
| 3 |
| 4 |
| 1 |
| 12 |
乙、丙两人都回答对的概率是
| 1 |
| 4 |
记“甲回答对这道题”、“乙回答对这道题”、
“丙回答对这道题”分别为事件A、B、C,
则P(A)=
| 3 |
| 4 |
且有
|
即
|
∴P(B)=
| 3 |
| 8 |
| 2 |
| 3 |
(Ⅱ)答对该题的人数ξ,ξ的可能取值:0,1,2,3,
根据相互独立事件的概率公式得到
P(ξ=0)=P(
| . |
| A |
| . |
| B |
| . |
| C |
| 5 |
| 96 |
P(ξ=1)=P(A•
| . |
| B |
| . |
| C |
| . |
| A |
| . |
| B |
| . |
| C |
| . |
| A |
| . |
| B |
| 7 |
| 24 |
P(ξ=2)=P(A•B•
| . |
| C |
| . |
| B |
| . |
| A |
| 15 |
| 32 |
P(ξ=3)=P(A•B•C)=
| 3 |
| 16 |
∴ξ的分布列是

∴Eξ=1×
| 7 |
| 24 |
| 15 |
| 32 |
| 3 |
| 16 |
| 43 |
| 24 |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
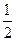 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是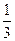 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求: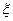 的分布列和数学期望.
的分布列和数学期望. ,
, ,执行右边程序框图,则输出的结果共有( )
,执行右边程序框图,则输出的结果共有( )