题目内容
曲线 在点
在点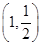 处的切线方程为 ( )
处的切线方程为 ( )
A.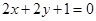 | B.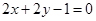 |
C.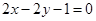 | D.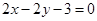 |
C
解析试题分析:因为 ,所以切线的斜率
,所以切线的斜率 。由直线的点斜式方程得切线的方程为
。由直线的点斜式方程得切线的方程为 ,即
,即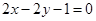 。故选C。
。故选C。
考点:导数的几何意义;直线的点斜式方程
点评:求曲线的切线方程是常考知识点,这类题目不难。通过学习导数,我们知道,函数在某点处的导数就是该点切线的斜率。

练习册系列答案
相关题目
若曲线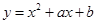 在点
在点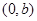 处的切线方程是
处的切线方程是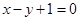 ,则( )
,则( )
A.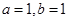 | B.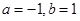 |
C.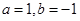 | D.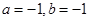 |
设函数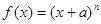 ,其中
,其中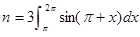 ,
,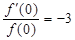 ,则
,则 的展开式中
的展开式中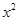 的系数为( )
的系数为( )
A.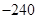 | B.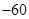 | C.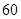 | D.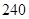 |
若函数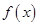 在R 上可导,且满足
在R 上可导,且满足 ,则( )
,则( )
A.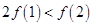 | B.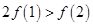 | C.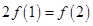 | D.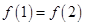 |
若函数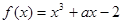 在区间
在区间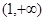 内是增函数,则实数
内是增函数,则实数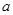 的取值范围是 ( )
的取值范围是 ( )
A.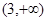 | B.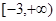 | C.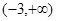 | D.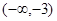 |
设曲线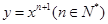 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为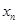 ,则
,则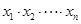 的值为
的值为
A.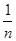 | B.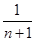 | C.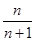 | D.1 |
一个物体的运动方程为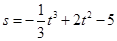 ,其中
,其中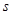 的单位是米,
的单位是米,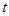 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.3米/秒 | B.6米/秒 | C.5米/秒 | D.4米/秒 |
设函数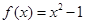 ,则
,则 在
在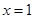 处的导数
处的导数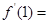 ( )
( )
A.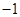 | B.0 | C.1 | D.2 |
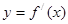 的图象可能是( )
的图象可能是( )