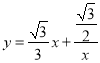Question

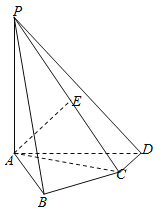
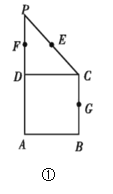
【题目】如图①在直角梯形ABCP中，，，，，E，F，G分别是线段PC，PD，BC的中点，现将折起，使平面平面ABCD如图②.

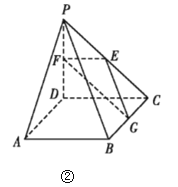
（1）求证:平面EFG；

（2）求二面角G—EF—D的大小.

Answer 1

【答案】（1）证明见解析（2）

【解析】

(1) 以D坐标原点直线DADCDP分别为x,y与z轴建立空间直角坐标系,再计算平面的法向量,证明即可.

(2)根据(1)中建立的空间直角坐标系,利用空间向量求解二面角大小即可.

（1）在图②中,平面平面ABCD,平面平面, 平面ABCD,,如图以D坐标原点直线DADCDP分别为x,y与z轴建立空间直角坐标系,则有,

,设平面GEF用法向量,由法向量的定义得: ,不妨设,所以,则, 点平面EFG,平面EFG.

（2）由（1）知平面GEF法向量,因平面EFD与坐标平面PDC重合,则它的一个法向量为,设二面角G-EF-D为,则由图观察二面角G-EF-D锐角, .故二面角G-EF-D的大小为.

解法二:（1）,根据面面平行的判定定理, 平面平面PAB,又面PAB, 平面EFG.

（2）平面平面ABCD,, 平面PCD,而面EFD过C作交长线于R点连GR,根据三垂线定理知即为二面角的平面角, ,故二面角G-EF-D大小为.