题目内容
12.解下列不等式:(1)$\frac{x-1}{x-2}>\frac{1}{2}$
(2)x2-x+a-a2<0.
分析 (1)直接利用分式不等式转化为二次不等式求解即可.
(2)通过分解因式通过对应方程的根的大小,求解不等式即可.
解答 解:(1)由题意得$\frac{x}{2(x-2)}>0$(3分)
解集为(-∞,0)∪(2,+∞)(5分)
(2)、由题意得(x-a)(x-1+a)<0,
∴当a<1-a时,即$a<\frac{1}{2}$时,解集为(a,1-a)
当a>1-a时,即$a>\frac{1}{2}$时,解集为(1-a,a)(7分)
当a=1-a时,即$a=\frac{1}{2}$时,解集为∅(10分)
点评 本题考查分式不等式的解法,二次不等式的解法,考查分类讨论思想以及转化思想的应用.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
2.设集合A={x|0≤x≤4},B={y|y=-x2,-1≤x≤2},则∁R(A∩B)=( )
| A. | R | B. | {x|x∈R,x≠0} | C. | {0} | D. | ∅ |
20.己知程序框图如图所示,执行相应程序,若输出S=15,则框图中①处可以填入( )


| A. | n≥4? | B. | n>8? | C. | n>4? | D. | n≥8? |
2.已知a>0且a≠1,则使关于x的方程loga(x-2ak)=loga(x2-a2)有解的k的取值范围是( )
| A. | 0<k<$\frac{1}{2}$或k$<-\frac{1}{2}$ | B. | 0<k<1或k<-1 | C. | 0<k<2或k<-2 | D. | 0<k<1或k<-2 |
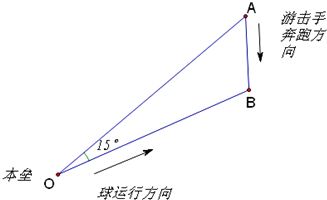 在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)
在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)