题目内容
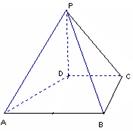
如图,平面ABCD⊥平面ABEF,又ABCD是正方形,ABEF是矩形,且 G是EF的中
G是EF的中
点.
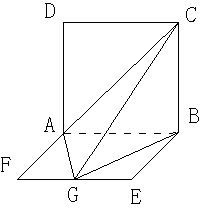
(1)求证:平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角的正弦值.
 G是EF的中
G是EF的中点.

(1)求证:平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角的正弦值.
(1)先证AG⊥平面CBG (2)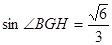
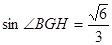
试题分析:(1)证.正方形ABCD
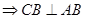 ,∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF
,∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF ∵AG,GB
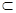 面ABEF, ∴CB⊥AG,CB⊥BG.又AD=2a,AF= a, ABEF是矩形,G是EF的中点.
面ABEF, ∴CB⊥AG,CB⊥BG.又AD=2a,AF= a, ABEF是矩形,G是EF的中点.∴AG=BG=
 ,AB=2a, AB2=AG2+BG2, ∴AG⊥BG,∵BC∩BG=B,∴AG⊥平面CBG,而AG
,AB=2a, AB2=AG2+BG2, ∴AG⊥BG,∵BC∩BG=B,∴AG⊥平面CBG,而AG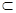 面AGC,故平
面AGC,故平面AGC⊥平面BGC.
(2)解.如图,由(1)知面AGC⊥面BGC,且交于GC,在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,
∴∠BGH是GB与平面AGC所成的角.
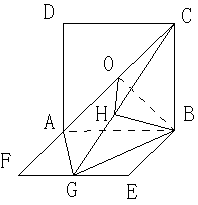
∴在R t△CBG中

又BG=
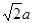 ,∴
,∴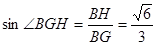
点评:本题考查面面垂直的判定方法,以及求线面成的角的求法,体现转化的思想.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
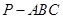 的底面
的底面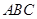 是直角三角形,且
是直角三角形,且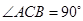 ,
,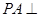 平面
平面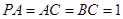 ,
,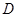 是线段
是线段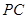 的中点,如图所示.
的中点,如图所示.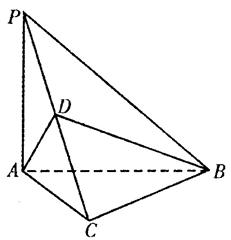
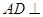 平面
平面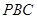 ;
;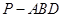 的体积.
的体积. 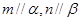 且
且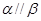 ,则
,则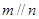 ;②若
;②若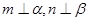 且
且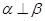 ,则
,则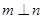 ;
; 且
且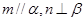 且
且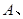 ①②
①②  ③④
③④  ①④
①④  ②③
②③ 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则
 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,若
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若 ,则AB与平面β所成的角的正弦值是( )
,则AB与平面β所成的角的正弦值是( )




 是直线,
是直线, 是两个不同的平面,下列命题成立的是( )
是两个不同的平面,下列命题成立的是( ) ,则
,则
 ∥
∥ ,则
,则 ,
, , 则
, 则 中,
中, ,
, ,
, 是角平分线。求证:
是角平分线。求证: 。
。