��Ŀ����
������������D�ϵĺ���y=f��x����������D�ϵ���������ֵx1��x2�������²���ʽ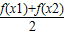 ��f��
��f��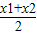 ����������ƺ���y=f��x��Ϊ����D�ϵ�������
����������ƺ���y=f��x��Ϊ����D�ϵ���������1��֤����������R�ϵĶ��κ���f��x��=ax2+bx+c��a��0����������
��2����f��x��=ax2+x��a��R��a��0��������x��[0��1]ʱ��f��x����1���������ʵ��a��ȡֵ��Χ�����жϺ���
f��x��=ax2+x��a��R��a��0���ܷ��ΪR�ϵ�������
��3��������������Z�ϵĺ���f��x�����㣺�ٶ������x��y��Z��f��x+y��=f��x��f��y������f��0����0��f��1��=2��
����f��x���Ľ���ʽ�����ж�����ĺ���f��x���Dz���R�ϵ�����˵�����ɣ�
���𰸡���������1���������֤������Ҫ֤�� ��ֻҪ֤��
��ֻҪ֤�� ��
��
��2�����ȸ����Ա����ķ�Χ���з��볣����Ȼ�������ת��Ϊ��������ֵ�����⣬����ֵʱ�����䷽��������a�ķ�Χ�ͣ�1���ж��Ƿ�Ϊ������
��3��������x=y=0�����f��0����ֵ������y=-x���ɵó�f��x����f��-x��֮��Ĺ�ϵ���������������ϵ���ó�f��n����f��1���Ĺ�ϵ���Ϳɵó�f��x���Ľ���ʽ�������û�������ʽ�ж��Ƿ�Ϊ������
����⣺��1��֤����������x1��x2��R����a��0��
��[f��x1��+f��x2��]-2f�� ��=ax12+bx1+c+ax22+bx2+c-2[a��
��=ax12+bx1+c+ax22+bx2+c-2[a�� ��2+b��
��2+b�� ��+c]=ax12+ax22-
��+c]=ax12+ax22- a��x12+x22+2x1x2��=
a��x12+x22+2x1x2��= a��x1-x2��2 ��3�֣�
a��x1-x2��2 ��3�֣�
�൱a��0ʱ��f��x1��+f��x2����2f�� ������
������ ��f��
��f�� ��
��
��a��0ʱ������f��x���������� ��5�֣�
��2����x=0ʱ������a��R����f��x����1���������x�ʣ�0��1]ʱ��Ҫf��x����1���������ax2��-x+1��
��a�� -
- =��
=�� -
- ��2-
��2- ���������x�ʣ�0��1]����
���������x�ʣ�0��1]���� ��1����
��1���� =1ʱ����
=1ʱ���� -
- ��2-
��2- ȡ����СֵΪ0��
ȡ����СֵΪ0��
��a��0����a��0����a��ȡֵ��Χ�ǣ�-�ޣ�0����
�ɴ˿�֪������������ʵ��a��ȡֵ��Ϊ�������ɣ�1����֪����f��x�������� ��11�֣�
��3����x=y=0����f��0��=[f��0��]2����f��0����0����f��0��=1����12�֣�
��y=-x����1=f��0��=f��x-x��=f��x��f��-x������f��x��= ��
��
��n��N*����f��n��=f[��n-1��+1]=f��n-1��f��1��=2f��n-1��=��=[f��1��]2�� ��14�֣�
��n��0��n��Z����-n��N*����f��n��= =
= =2n����x��Zʱ��f��x��=2x��
=2n����x��Zʱ��f��x��=2x��
�����������������x��Z������f��x��=2x�� ��15�֣�
�� [2+21]=
[2+21]= ��
�� ������f��x������R�ϵ������� ��16�֣�
������f��x������R�ϵ������� ��16�֣�
��������x1��x2��R���� [f��x1��+f��x2��]=
[f��x1��+f��x2��]= [
[ ]��
]�� ×2
×2 =f��
=f�� ��������f��x������R�ϵ������� 16�֣�
��������f��x������R�ϵ������� 16�֣�
�����������������ѧ�¶������������ж�һ������������Ҫ���ݶ��壬�����ǡ������������ĵ�һ����ڶ��ʽ�����ϵ������Ҫץס��һ�㣮�ѵ��ڵ����ʣ�������x��y��ֵ���������úâٺ͢ڣ������������ʽ��
 ��ֻҪ֤��
��ֻҪ֤�� ��
����2�����ȸ����Ա����ķ�Χ���з��볣����Ȼ�������ת��Ϊ��������ֵ�����⣬����ֵʱ�����䷽��������a�ķ�Χ�ͣ�1���ж��Ƿ�Ϊ������
��3��������x=y=0�����f��0����ֵ������y=-x���ɵó�f��x����f��-x��֮��Ĺ�ϵ���������������ϵ���ó�f��n����f��1���Ĺ�ϵ���Ϳɵó�f��x���Ľ���ʽ�������û�������ʽ�ж��Ƿ�Ϊ������
����⣺��1��֤����������x1��x2��R����a��0��
��[f��x1��+f��x2��]-2f��
 ��=ax12+bx1+c+ax22+bx2+c-2[a��
��=ax12+bx1+c+ax22+bx2+c-2[a�� ��2+b��
��2+b�� ��+c]=ax12+ax22-
��+c]=ax12+ax22- a��x12+x22+2x1x2��=
a��x12+x22+2x1x2��= a��x1-x2��2 ��3�֣�
a��x1-x2��2 ��3�֣��൱a��0ʱ��f��x1��+f��x2����2f��
 ������
������ ��f��
��f�� ��
����a��0ʱ������f��x���������� ��5�֣�
��2����x=0ʱ������a��R����f��x����1���������x�ʣ�0��1]ʱ��Ҫf��x����1���������ax2��-x+1��
��a��
 -
- =��
=�� -
- ��2-
��2- ���������x�ʣ�0��1]����
���������x�ʣ�0��1]���� ��1����
��1���� =1ʱ����
=1ʱ���� -
- ��2-
��2- ȡ����СֵΪ0��
ȡ����СֵΪ0����a��0����a��0����a��ȡֵ��Χ�ǣ�-�ޣ�0����
�ɴ˿�֪������������ʵ��a��ȡֵ��Ϊ�������ɣ�1����֪����f��x�������� ��11�֣�
��3����x=y=0����f��0��=[f��0��]2����f��0����0����f��0��=1����12�֣�
��y=-x����1=f��0��=f��x-x��=f��x��f��-x������f��x��=
 ��
����n��N*����f��n��=f[��n-1��+1]=f��n-1��f��1��=2f��n-1��=��=[f��1��]2�� ��14�֣�
��n��0��n��Z����-n��N*����f��n��=
 =
= =2n����x��Zʱ��f��x��=2x��
=2n����x��Zʱ��f��x��=2x�������������������x��Z������f��x��=2x�� ��15�֣�
��
 [2+21]=
[2+21]= ��
�� ������f��x������R�ϵ������� ��16�֣�
������f��x������R�ϵ������� ��16�֣���������x1��x2��R����
 [f��x1��+f��x2��]=
[f��x1��+f��x2��]= [
[ ]��
]�� ×2
×2 =f��
=f�� ��������f��x������R�ϵ������� 16�֣�
��������f��x������R�ϵ������� 16�֣������������������ѧ�¶������������ж�һ������������Ҫ���ݶ��壬�����ǡ������������ĵ�һ����ڶ��ʽ�����ϵ������Ҫץס��һ�㣮�ѵ��ڵ����ʣ�������x��y��ֵ���������úâٺ͢ڣ������������ʽ��

��ϰ��ϵ�д�
�����Ŀ

 �ĵ����ԣ�
�ĵ����ԣ�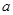 ��ȡֵ��Χ��
��ȡֵ��Χ��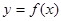 ��������D�ϵ���������ֵx1��x2�������²���ʽ
��������D�ϵ���������ֵx1��x2�������²���ʽ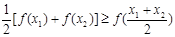 ��������ƺ���
��������ƺ��� �����жϺ���
�����жϺ��� ��
�� ��������ƺ���y=f��x��Ϊ����D�ϵġ����� ��������֤��a��0ʱ��f��x��Ϊ������������
��������ƺ���y=f��x��Ϊ����D�ϵġ����� ��������֤��a��0ʱ��f��x��Ϊ������������ ��
�� ��������ƺ���y=f��x��Ϊ����D�ϵġ����� ��������֤��a��0ʱ��f��x��Ϊ������������
��������ƺ���y=f��x��Ϊ����D�ϵġ����� ��������֤��a��0ʱ��f��x��Ϊ������������