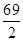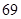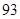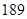题目内容
已知等差数列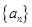 的前
的前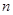 项和为
项和为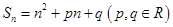 ,且
,且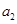 、
、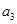
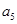 成等比数列.
成等比数列.
(1)求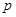 、
、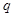 的值;
的值;
(2)若数列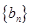 满足
满足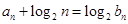 ,求数列
,求数列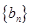 的前
的前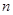 项和
项和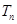 .
.
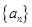 的前
的前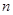 项和为
项和为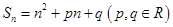 ,且
,且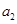 、
、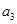
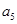 成等比数列.
成等比数列.(1)求
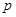 、
、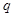 的值;
的值;(2)若数列
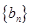 满足
满足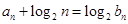 ,求数列
,求数列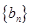 的前
的前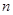 项和
项和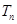 .
.(1)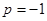 ,
,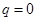 ;(2)
;(2)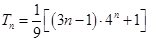 .
.
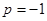 ,
,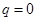 ;(2)
;(2)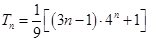 .
.试题分析:(1)解法1是先令
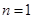 求出
求出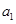 的表达式,然后令
的表达式,然后令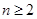 ,得到
,得到 计算出
计算出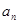 在
在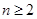 的表达式,利用
的表达式,利用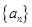 为等差数列得到
为等差数列得到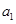 满足通式,从而求出
满足通式,从而求出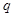 的值,然后利用条件
的值,然后利用条件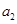 、
、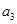
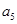 成等比数列列方程求出
成等比数列列方程求出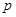 的值,从而求出
的值,从而求出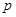 、
、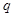 的值;解法2是在数列
的值;解法2是在数列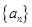 是等差数列的前提下,设其公差为
是等差数列的前提下,设其公差为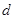 ,利用公式
,利用公式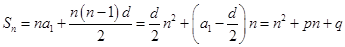 以及对应系数相等的特点得到
以及对应系数相等的特点得到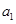 、
、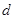 和
和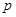 、
、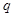 之间的等量关系,然后利用条件
之间的等量关系,然后利用条件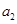 、
、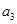
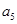 成等比数列列方程求出
成等比数列列方程求出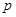 的值,从而求出
的值,从而求出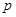 、
、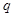 的值;(2)解法1是在(1)的前提下求出数列
的值;(2)解法1是在(1)的前提下求出数列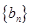 的通项公式,然后利用错位相减法求数列
的通项公式,然后利用错位相减法求数列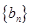 的和;解法2是利用导数
的和;解法2是利用导数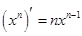 以及函数和的导数运算法则,将数列
以及函数和的导数运算法则,将数列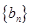 的前
的前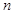 项和
项和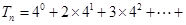
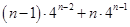 视为函数列
视为函数列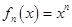 的前
的前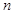 项和在
项和在 处的导数值,从而求出
处的导数值,从而求出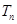 .
.试题解析:(1)解法1:当
 时,
时,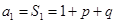 ,
,当
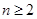 时,
时,
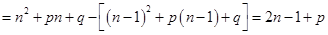 .
.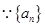 是等差数列,
是等差数列,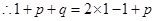 ,得
,得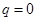 .
.又
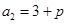 ,
, ,
,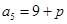 ,
,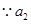 、
、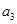 、
、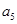 成等比数列,
成等比数列,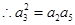 ,即
,即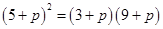 ,解得
,解得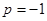 .
.解法2:设等差数列
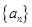 的公差为
的公差为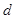 ,
,则
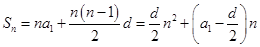 .
.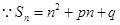 ,
,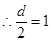 ,
,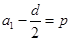 ,
,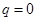 .
.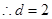 ,
,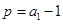 ,
,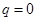 .
.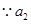 、
、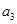 、
、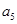 成等比数列,
成等比数列,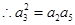 ,
,即
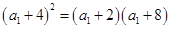 ,解得
,解得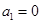 .
.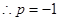 ;
;(2)解法1:由(1)得
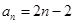 .
.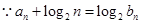 ,
,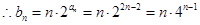 .
.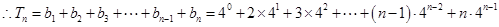 ,①
,①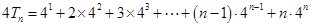 ,②
,②①
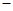 ②得
②得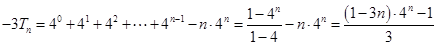 .
.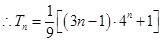 .
.解法2:由(1)得
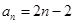 .
.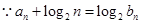 ,
,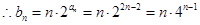 .
.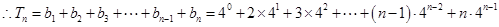 ,①
,①由
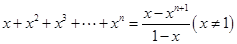 ,
,两边对
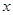 取导数得,
取导数得,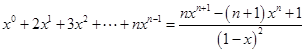 .
.令
 ,得
,得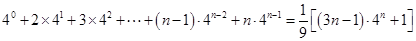 .
.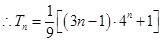 .
.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
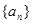 的前
的前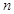 项和为
项和为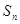 ,对一切正整数
,对一切正整数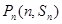 都在函数
都在函数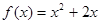 的图象上.
的图象上.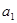 ,
,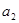 ;
;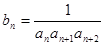 ,求证数列
,求证数列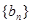 的前
的前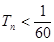 .
.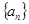 ,
,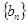 ,
,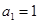 ,
,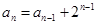 ,
,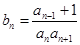 ,
,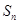 为数列
为数列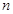 项和,
项和,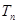 为数列
为数列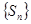 的前
的前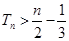 .
.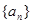 中,
中,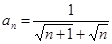 (其中
(其中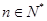 ),若其前n项和
),若其前n项和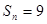 ,则
,则 .
. 与
与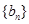 满足
满足 ,且
,且 ,设数列
,设数列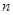 项和为
项和为 ,则
,则 =.
=. 的前
的前 项和为
项和为 ,若
,若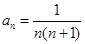 ,则
,则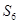 等于( )
等于( )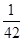
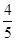
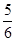
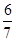
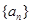 是由正数组成的等比数列,
是由正数组成的等比数列,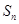 表示
表示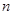 项的和,若
项的和,若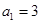 ,
,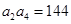 ,则
,则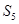 的值是 ( )
的值是 ( )