题目内容
(本题满分15分)
已知:函数![]() 对一切实数
对一切实数![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值。 w.w.w.k.s.5.u.c.o.m
的值。 w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求![]() 的解析式。
的解析式。
(3)已知![]() ,设P:当
,设P:当![]() 时,不等式
时,不等式![]() 恒成立;Q:当
恒成立;Q:当![]() 时,
时,![]() 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的![]() 的集合记为
的集合记为![]() ,满足Q成立的
,满足Q成立的![]() 的集合记为
的集合记为![]() ,求
,求![]() ∩
∩![]() (
(![]() 为全集)。
为全集)。
解析:(1)令![]() ,则由已知
,则由已知![]()
∴![]() (3分)
(3分)
(2)令![]() , 则
, 则![]()
又∵![]()
∴![]() (3分)
(3分)
(3)不等式![]() 即
即![]()
即![]()
当![]() 时,
时,![]() , 又
, 又![]() 恒成立
恒成立
故![]() (3分)
(3分)
![]()
又![]() 在
在![]() 上是单调函数,故有
上是单调函数,故有![]()
∴![]() (3分)
(3分)
∴![]() ∩
∩![]() =
=![]() (3分)
(3分)

练习册系列答案
相关题目
 (0,1),
(0,1), ,直线
,直线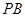 、
、 都是圆
都是圆 的切线(
的切线(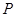 点不在
点不在 轴上).
轴上). 轴上的抛物线的标准方程;
轴上的抛物线的标准方程; 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使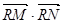 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由 ,命题q:
,命题q: . 若“p且q”为真命题,求实数m的取值范围.
. 若“p且q”为真命题,求实数m的取值范围. 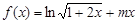 .
.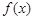 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围; 时,求函数
时,求函数 ,且
,且 时,证明:
时,证明: .
. 和抛物线C:
和抛物线C: ,圆的切线
,圆的切线 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B, 对称,问是否存在直线
对称,问是否存在直线 ?若存在,求出直线
?若存在,求出直线
 ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值; ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]