题目内容
已知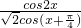 =
= ,0<x<π,则tanx为
,0<x<π,则tanx为
- A.-

- B.-

- C.2
- D.-2
A
分析:将已知等式左边分子利用二倍角的余弦函数公式化简,分母利用两角和与差的余弦函数公式及特殊角的三角函数值化简,整理后约分得到cosx+sinx= ,再将此等式左右两边平方,利用同角三角函数间的基本关系化简,求出2sinxcosx的值小于0,由x的范围得到sinx大于0,cosx小于0,再利用完全平方公式及同角三角函数间的基本关系求出cosx-sinx的值,与sinx+cosx的值联立组成方程组,求出方程组的解得到sinx与cosx的值,进而确定出tanx的值.
,再将此等式左右两边平方,利用同角三角函数间的基本关系化简,求出2sinxcosx的值小于0,由x的范围得到sinx大于0,cosx小于0,再利用完全平方公式及同角三角函数间的基本关系求出cosx-sinx的值,与sinx+cosx的值联立组成方程组,求出方程组的解得到sinx与cosx的值,进而确定出tanx的值.
解答:∵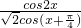 =
=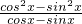 =cosx+sinx=
=cosx+sinx= ①,
①,
∴(cosx+sinx)2= ,即sin2x+2sinxcosx+cos2x=1+2sinxcosx=
,即sin2x+2sinxcosx+cos2x=1+2sinxcosx= ,
,
∴2sinxcosx=- <0,又0<x<π,
<0,又0<x<π,
∴sinx>0,cosx<0,
∴(cosx-sinx)2=sin2x-2sinxcosx+cos2x=1-2sinxcosx= ,
,
∴cosx-sinx=- ②,
②,
联立①②解得:cosx=- ,sinx=
,sinx= ,
,
则tanx=- .
.
故选A
点评:此题考查了二倍角的余弦函数公式,两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.
分析:将已知等式左边分子利用二倍角的余弦函数公式化简,分母利用两角和与差的余弦函数公式及特殊角的三角函数值化简,整理后约分得到cosx+sinx=
 ,再将此等式左右两边平方,利用同角三角函数间的基本关系化简,求出2sinxcosx的值小于0,由x的范围得到sinx大于0,cosx小于0,再利用完全平方公式及同角三角函数间的基本关系求出cosx-sinx的值,与sinx+cosx的值联立组成方程组,求出方程组的解得到sinx与cosx的值,进而确定出tanx的值.
,再将此等式左右两边平方,利用同角三角函数间的基本关系化简,求出2sinxcosx的值小于0,由x的范围得到sinx大于0,cosx小于0,再利用完全平方公式及同角三角函数间的基本关系求出cosx-sinx的值,与sinx+cosx的值联立组成方程组,求出方程组的解得到sinx与cosx的值,进而确定出tanx的值.解答:∵
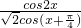 =
=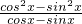 =cosx+sinx=
=cosx+sinx= ①,
①,∴(cosx+sinx)2=
 ,即sin2x+2sinxcosx+cos2x=1+2sinxcosx=
,即sin2x+2sinxcosx+cos2x=1+2sinxcosx= ,
,∴2sinxcosx=-
 <0,又0<x<π,
<0,又0<x<π,∴sinx>0,cosx<0,
∴(cosx-sinx)2=sin2x-2sinxcosx+cos2x=1-2sinxcosx=
 ,
,∴cosx-sinx=-
 ②,
②,联立①②解得:cosx=-
 ,sinx=
,sinx= ,
,则tanx=-
 .
.故选A
点评:此题考查了二倍角的余弦函数公式,两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知p:0<x<2,q:
≥1,则¬p是¬q的( )
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |