题目内容
设直线l(斜率存在)交抛物线y2=2px(p>0,且p是常数)于两个不同点A(x1,y1),B(x2,y2),O为坐标原点,且满足| OA |
| OB |
(1)若y1+y2=-1,求直线l的斜率与p之间的关系;
(2)求证:直线l过定点;
(3)设(1)中的定点为P,若点M在射线PA上,满足
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
|
分析:(1)设直线l的方程为y=kx+b,由
,得ky2-2py+2pb=0,再由根的判别式和根与系数的关系,可知直线l的斜率与p之间的关系.
(2)由题设知,y1y2=2(y1+y2).则
=2×
,得b=2.所以直线l的方程为y=kx+2.由此知直线l过定点(0,2).
(3)分别过点A、M、B向y轴作垂线,垂足分别为A‘,M’,B‘,设M(x,y),由
=
+
,可得
=
+
.所以
=
+
.由此入手可求出点M的轨迹方程.
|
(2)由题设知,y1y2=2(y1+y2).则
| 2pb |
| k |
| 2p |
| k |
(3)分别过点A、M、B向y轴作垂线,垂足分别为A‘,M’,B‘,设M(x,y),由
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
|
| 1 |
| |2-y| |
| 1 |
| |2-y1| |
| 1 |
| |2-y2| |
解答:解:(1)设直线l的方程为y=kx+b,由
,得ky2-2py+2pb=0,
由题知k≠0,△=4p2-8kpb>0,且y1+y2=
.
又y1+y2=-1,∴k=-2p.
∴直线l的斜率k与p之间的关系为k=-p.
(2)由(1),有
,
又
•
=x1x2+y1y2=x1x2+2(y1+y2),
∴y1y2=2(y1+y2).则
=2×
,得b=2.
∴直线l的方程为y=kx+2.
∴直线l过定点(0,2).
(3)分别过点A、M、B向y轴作垂线,垂足分别为A′,M′,B′,
设M(x,y),由
=
+
,
可得
=
+
.
∴
=
+
,∴
=
+
.
∴
=
=
=1-
,
∴
=1-
×
=1-
,∴2k=
×p,
∵△=4p2-16kp>0,∴1<y<3,y≠2.
∵y=kx+2,∴y=
x+1(1<y<3,y≠2).
∴点M的轨迹方程为y=
x+1(1<y<3,y≠2).
|
由题知k≠0,△=4p2-8kpb>0,且y1+y2=
| 2p |
| k |
又y1+y2=-1,∴k=-2p.
∴直线l的斜率k与p之间的关系为k=-p.
(2)由(1),有
|
又
| OA |
| OB |
∴y1y2=2(y1+y2).则
| 2pb |
| k |
| 2p |
| k |
∴直线l的方程为y=kx+2.
∴直线l过定点(0,2).
(3)分别过点A、M、B向y轴作垂线,垂足分别为A′,M′,B′,
设M(x,y),由
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
|
可得
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
|
∴
| 1 |
| |2-y| |
| 1 |
| |2-y1| |
| 1 |
| |2-y2| |
| 1 |
| 2-y |
| 1 |
| 2-y1 |
| 1 |
| 2-y2 |
∴
| 1 |
| 2-y |
| 4-(y1+y2) |
| 4-2(y1+y2)+y1y2 |
| 4-(y1+y2) |
| 4-2(y1+y2)+2(y1+y2) |
| y1+y2 |
| 4 |
∴
| 1 |
| 2-y |
| 1 |
| 4 |
| 2p |
| k |
| p |
| 2k |
| 2-y |
| 1-y |
∵△=4p2-16kp>0,∴1<y<3,y≠2.
∵y=kx+2,∴y=
| p |
| 2 |
∴点M的轨迹方程为y=
| p |
| 2 |
点评:本题考查直线与圆锥曲线的综合应用问题,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 =x1x2+2(y1+y2).
=x1x2+2(y1+y2). ,求点M
,求点M =x1x2+2(y1+y2).
=x1x2+2(y1+y2). ,求点M的轨迹方程.
,求点M的轨迹方程. =x1x2+2(y1+y2).
=x1x2+2(y1+y2).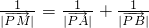 ,求点M的轨迹方程.
,求点M的轨迹方程.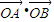 =x1x2+2(y1+y2).
=x1x2+2(y1+y2).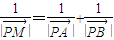 ,求点M的轨迹方程.
,求点M的轨迹方程.