题目内容
(本小题满分10分)选修4—1:几何证明选讲
如图,四边形ACED是圆内接四边形,延长AD与CE的延长线交于点B,且AD=DE,AB=2AC.

(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=2,BC=4时,求AD的长.
(1)见解析;(2)AD=
【解析】试题解析:(1)∵四边形ACDE为圆内接四边形,∴∠BDE=∠BCA
∵∠DBE=∠CBA,
∴△BDE∽△BCA,则
∵AB=2AC
∴BE=2DE,结合AD=DE,可得BE=2AD
(2)易知,AB=2AC=4
由切割定理得BD·BA=BE·BC,即(AB-AD)·BA=2AD·4
可得(4-AD)·4=2AD·4,解得AD=
考点:本题考查几何证明

练习册系列答案
相关题目
 ,命题
,命题 ,则
,则 是真命题,
是真命题,
 :
: 

 ,则下列目标函数中,在点
,则下列目标函数中,在点 处取得最小值得是( )
处取得最小值得是( ) (B)
(B)
 (D)
(D)
 中,则
中,则
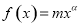 的图象经过点
的图象经过点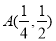 ,则它在点A处的切线方程是( )
,则它在点A处的切线方程是( )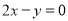 B.
B.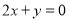
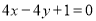 D.
D.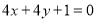
 .
. ,求a,b;
,求a,b; ,求b.
,求b. 的图像如图所示(其中
的图像如图所示(其中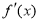 是定义域为R函数
是定义域为R函数 的导函数),则以下说法错误的是( )
的导函数),则以下说法错误的是( )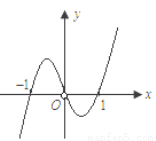
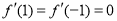
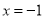 时, 函数
时, 函数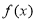 取得极大值[]
取得极大值[]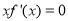 与
与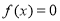 均有三个实数根 []
均有三个实数根 []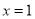 时,函数
时,函数 满足
满足 则
则 =________
=________ 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且 。
。 ;
; ,求
,求