题目内容
从双曲线
-
=1(a>0,b>0)上任意一点P引实轴平行线交两渐近线于Q,R两点,则|PQ|•|PR|之值为
| x2 |
| a2 |
| y2 |
| b2 |
a2
a2
.分析:设P(x0,y0),可得Q(x1,y0),R(x2,y0),分别联立方程可得x1=
y0,x2=-
y0,代入可得|PQ|•|PR|=|x1-x0|•|x2-x0|,结合P(x0,y0)在双曲线
-
=1上,代入消元可得.
| a |
| b |
| a |
| b |
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:设P(x0,y0),可得Q(x1,y0),R(x2,y0).
又可得渐近线方程为y=±
x,
联立
,解之可得x1=
y0
同理可得x2=-
y0,
故|PQ|•|PR|=|x1-x0|•|x2-x0|
=|(
y0-x0)(-
y0-x0)|=|x02-
y02|,
又P(x0,y0)在双曲线
-
=1上,故
-
=1,
变形可得x02=(1+
)a2,代入上式可得
|PQ|•|PR|=|x02-
y02|=a2
故答案为:a2
又可得渐近线方程为y=±
| b |
| a |
联立
|
| a |
| b |
同理可得x2=-
| a |
| b |
故|PQ|•|PR|=|x1-x0|•|x2-x0|
=|(
| a |
| b |
| a |
| b |
| a2 |
| b2 |
又P(x0,y0)在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| x02 |
| a2 |
| y02 |
| b2 |
变形可得x02=(1+
| y02 |
| b2 |
|PQ|•|PR|=|x02-
| a2 |
| b2 |
故答案为:a2
点评:本题考查双曲线的简单性质,涉及设而不求的思想,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
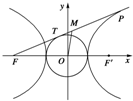 如图,从双曲线
如图,从双曲线| x2 |
| a2 |
| y2 |
| b2 |
| A、|MO|-|MT|>b-a |
| B、|MO|-|MT|<b-a |
| C、|MO|-|MT|=b-a |
| D、以上三种可能都有 |
从双曲线
-
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|-|MT|与b-a的关系为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、|MO|-|MT|>b-a |
| B、|MO|-|MT|<b-a |
| C、|MO|-|MT|=b-a |
| D、|MO|-|MT|与b-a无关 |
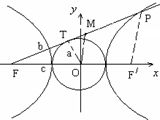 从双曲线
从双曲线