题目内容
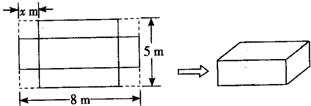
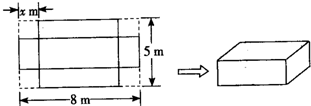 如图所示,将一个长为8m,宽为5m的长方形剪去四个相同的边长为xm的正方形,然后再将所得图形围成一个无盖长方体,试求x为多少时,长方体的体积最大?最大体积为多少?
如图所示,将一个长为8m,宽为5m的长方形剪去四个相同的边长为xm的正方形,然后再将所得图形围成一个无盖长方体,试求x为多少时,长方体的体积最大?最大体积为多少?分析:首先分析题目求长为8m,宽为5m的长方形铁皮做一个无盖长方体,当长方体的高为多少时,容积最大.故可根据边长为xm的正方形,求出长方体的体积f(x)关于x的方程,然后求出导函数,分析单调性即可求得最值.
解答:解:根据题意边长为xm的正方形,容器的体积为f(x),
则有V=f(x)=(8-2x)(5-2x)x=4x3-26x2+40x,(0<x<2.5)
求导可得到:V′=12x2-52x2+40,
由V′=12x2-52x2+40=0得x1=1,x2=
(舍去).
所以当x<1时,V′>0,
当1<x<
时,V′<0,
当x>
时,V′>0,
所以,当x=1,V有极大值f(1)=18,又f(0)=0,f(2.5)=0,
所以当x=1,V有最大值f(1)=18.
则有V=f(x)=(8-2x)(5-2x)x=4x3-26x2+40x,(0<x<2.5)
求导可得到:V′=12x2-52x2+40,
由V′=12x2-52x2+40=0得x1=1,x2=
| 10 |
| 3 |
所以当x<1时,V′>0,
当1<x<
| 10 |
| 3 |
当x>
| 10 |
| 3 |
所以,当x=1,V有极大值f(1)=18,又f(0)=0,f(2.5)=0,
所以当x=1,V有最大值f(1)=18.
点评:此题主要考查用代数式表示正方形、矩形的面积和体积、考查函数求最值在实际问题中的应用,其中涉及到由导函数分类讨论单调性的思想,在高考中属于重点考点,同学们需要理解并记忆.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
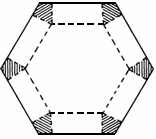

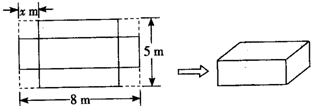 如图所示,将一个长为8m,宽为5m的长方形剪去四个相同的边长为xm的正方形,然后再将所得图形围成一个无盖长方体,试求x为多少时,长方体的体积最大?最大体积为多少?
如图所示,将一个长为8m,宽为5m的长方形剪去四个相同的边长为xm的正方形,然后再将所得图形围成一个无盖长方体,试求x为多少时,长方体的体积最大?最大体积为多少?