题目内容
甲、乙两名篮球运动员互不影响地在同一位置投球，命中率分别为
与
，且乙投球2次均未命中的概率为
。
（1）求乙投球的命中率。
（2）若甲投球1次，乙投球2次，两人共命中的次数记为
，求的分布列和数学期望。
与，且乙投球2次均未命中的概率为。（1）求乙投球的命中率
。（2）若甲投球1次，乙投球2次，两人共命中的次数记为
，求的分布列和数学期望。（1）乙投球的命中率为
（2）
的分布列为
的数学期望
（2）的分布列为 | 0 | 1 | 2 | 3 |
|  |  |  |  |
的数学期望本题考查离散型随机变量的分布列和期望，考查等可能事件的概率，考查对立事件的概率，是一个综合题，是近几年高考题目中经常出现的一个问题．
（Ⅰ）根据乙投球2次均未命中的概率为
，两次是否投中相互之间没有影响，根据相互独立事件的概率公式写出乙两次都未投中的概率，列出方程，解方程即可．
（II）做出甲投球命中的概率和乙投球命中的概率，因为两人共命中的次数记为ξ，得到变量可能的取值，看清楚变量对应的事件，做出事件的概率，写出分布列和期望
（Ⅰ）根据乙投球2次均未命中的概率为
，两次是否投中相互之间没有影响，根据相互独立事件的概率公式写出乙两次都未投中的概率，列出方程，解方程即可．（II）做出甲投球命中的概率和乙投球命中的概率，因为两人共命中的次数记为ξ，得到变量可能的取值，看清楚变量对应的事件，做出事件的概率，写出分布列和期望
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
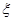的分布列，并求李明在一年内领到驾照的概率.
分，负者得
分，比赛进行到有一人比对方多
分或打满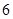
局时停止．设甲在每局中获胜的概率为
，且各局胜负相互独立．若第二局比赛结束时比赛停止的概率为
．
的值；
表示比赛停止时比赛的局数，求随机变量
。
，则关于
的方程
在
上有两个零点的概率为( )
