题目内容
【题目】若函数![]() 为定义域
为定义域![]() 上单调函数,且存在区间
上单调函数,且存在区间![]() (其中
(其中![]() ),使得当
),使得当![]() 时,
时,![]() 的取值范围恰为
的取值范围恰为![]() ,则称函数
,则称函数![]() 是
是![]() 上的正函数,区间
上的正函数,区间![]() 叫做等域区间.
叫做等域区间.
(1)已知![]() 是
是![]() 上的正函数,求
上的正函数,求![]() 的等域区间;
的等域区间;
(2)试探究是否存在实数![]() ,使得函数
,使得函数![]() 是
是![]() 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;
;
【解析】
试题分析:(1)由定义得当![]() 时,
时,![]() 代入解析式解方程组即可;(2)假设
代入解析式解方程组即可;(2)假设![]() 是区间
是区间![]() 上的正函数,因为函数
上的正函数,因为函数![]() 是
是![]() 上的减函数, 所以当
上的减函数, 所以当![]() 时,
时,![]() 即
即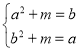 , 两式相减可得
, 两式相减可得![]() 代入
代入![]() 得
得![]() ,由
,由![]() 和
和![]() 得
得![]() ,故关于
,故关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有实数解,利用一元二次方程根的分布从对称轴、判别式和区间端点值三方面得不等式组解出即可;遇到这类题可以先画出符合的图像,在列不等式组比较好,否则容易漏解.
内有实数解,利用一元二次方程根的分布从对称轴、判别式和区间端点值三方面得不等式组解出即可;遇到这类题可以先画出符合的图像,在列不等式组比较好,否则容易漏解.
试题解析:(1)因为![]() 是
是![]() 上的正函数,且
上的正函数,且![]() 在
在![]() 上单调递增, 所以当
上单调递增, 所以当![]() 时,
时,![]() 即
即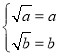 ,解锝
,解锝![]() ,故
,故![]() 的等域区间为
的等域区间为![]() .
.
(2)因为函数![]() 是
是![]() 上的减函数,
上的减函数,
所以当![]() 时,
时,![]() 即
即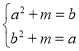
两式相减得![]() ,即
,即![]() ,
,
代入![]() 得
得![]() ,
,
由![]() ,且
,且![]() 得
得![]() ,
,
故关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有实数解,
内有实数解,
记![]() ,则
,则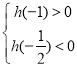 解得
解得![]() .
.

【题目】某地区甲校高二年级有1 100人,乙校高二年级有900人,为了统计两个学校高二年级在学业水平考试中的数学学科成绩,采用分层抽样的方法在两校共抽取了200名学生的数学成绩,如下表:(已知本次测试合格线是50分,两校合格率均为100%)
甲校高二年级数学成绩:
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 10 | 25 | 35 | 30 | x |
乙校高二年级数学成绩:
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 15 | 30 | 25 | y | 5 |
(1)计算x,y的值,并分别估计以上两所学校数学成绩的平均分(精确到1分).
(2)若数学成绩不低于80分为优秀,低于80分的为非优秀,根据以上统计数据写下面2×2列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“两个学校的数学成绩有差异?”
甲校 | 乙校 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |

