题目内容
在函数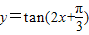
、y=|cosx|、
、
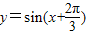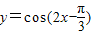中，最小正周期为π的函数的个数为（ ）A．1个
B．2个
C．3个
D．4个
【答案】分析：根据y=Atan（ωx+φ）的周期T=
，y=Asin（ωx+φ）和y=Acos（ωx+φ）的周期T=
，及函数图象的对折变换，分别求出各函数的周期，可得答案．
解答：解：∵函数
的ω=2，故其周期T=
y=cosx的周期为2π，将其图象沿x轴对折后得到y=|cosx|的图象，但周期变为原来的一半，故T=π
的ω=1，故其周期T=2π
的ω=2，故其周期T=π
故选B
点评：本题考查的知识点是三角函数的周期性及其求法，熟练掌握三角函数的周期是解答的关键．
，y=Asin（ωx+φ）和y=Acos（ωx+φ）的周期T=，及函数图象的对折变换，分别求出各函数的周期，可得答案．解答：解：∵函数
的ω=2，故其周期T=y=cosx的周期为2π，将其图象沿x轴对折后得到y=|cosx|的图象，但周期变为原来的一半，故T=π
的ω=1，故其周期T=2π的ω=2，故其周期T=π故选B
点评：本题考查的知识点是三角函数的周期性及其求法，熟练掌握三角函数的周期是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
若函数f（x）同时满足下列三个性质：
①最小正周期为π；
②图象关于直线x=
对称；
③在区间[-
，
]上是增函数．
则y=f（x）的解析式可以是（ ）
①最小正周期为π；
②图象关于直线x=
| π |
| 3 |
③在区间[-
| π |
| 6 |
| π |
| 3 |
则y=f（x）的解析式可以是（ ）
A、y=sin（2x-
| ||||
B、y=sin（
| ||||
C、y=cos（2x-
| ||||
D、y=cos（2x+
|