Question

【题目】已知点A（﹣1，0），B（1，0），C（0，1），直线y=ax+b（a＞0）将△ABC分割为面积相等的两部分，则b的取值范围是（ ）
A.（0，1）
B.
C.
D.

Answer 1

【答案】B
【解析】解：由题意可得，三角形ABC的面积为 =1，
由于直线y=ax+b（a＞0）与x轴的交点为M（﹣ ，0），
由直线y=ax+b（a＞0）将△ABC分割为面积相等的两部分，可得b＞0，
故﹣ ≤0，故点M在射线OA上．
设直线y=ax+b和BC的交点为N，则由 可得点N的坐标为（ ， ）．
①若点M和点A重合，则点N为线段BC的中点，故N（ ， ），
把A、N两点的坐标代入直线y=ax+b，求得a=b= ．
②若点M在点O和点A之间，此时b＞ ，点N在点B和点C之间，由题意可得三角形NMB的面积等于 ，
即 = ，即 = ，可得a= ＞0，求得 b＜ ，
故有 ＜b＜ ．
③若点M在点A的左侧，则b＜ ，由点M的横坐标﹣ ＜﹣1，求得b＞a．
设直线y=ax+b和AC的交点为P，则由 求得点P的坐标为（ ， ），
此时，由题意可得，三角形CPN的面积等于 ，即 （1﹣b）|xN﹣xP|= ，
即 （1﹣b）| ﹣ |= ，化简可得2（1﹣b）2=|a2﹣1|．
由于此时 b＞a＞0，0＜a＜1，∴2（1﹣b）2=|a2﹣1|=1﹣a2 ．
两边开方可得 （1﹣b）= ＜1，∴1﹣b＜ ，化简可得 b＞1﹣ ，
故有1﹣ ＜b＜ ．
再把以上得到的三个b的范围取并集，可得b的取值范围应是 ，
故选：B．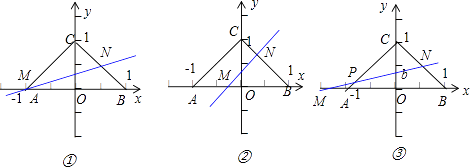

【考点精析】关于本题考查的点到直线的距离公式，需要了解点到直线的距离为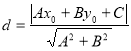：才能得出正确答案．