题目内容
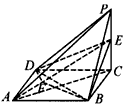
已知四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点,
(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(3)若点E为PC的中点,求二面角D-AE-B的大小.
(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(3)若点E为PC的中点,求二面角D-AE-B的大小.
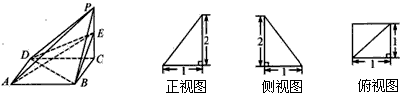
| 解:(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形, 侧棱PC⊥底面ABCD,且PC=2, ∴ 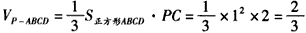 , ,即四棱锥P-ABCD的体积为 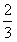 ; ;(2)不论点E在何位置,都有BD⊥AE; 证明如下:连接AC, ∵四边形ABCD是正方形, ∴BD⊥AC, ∵PC⊥底面ABCD,且BD 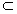 平面ABCD, 平面ABCD, ∴BD⊥PC, 又∵AC∩PC=C, ∴BD⊥平面PAC, ∵不论点E在何位置,都有AE 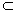 平面PAC, 平面PAC,∴不论点E在何位置,都有BD⊥AE; |
|
| (3)如图,在平面DAE内过点D作DF⊥AE于F,连接BF, ∵AD=AB=1,  , ,∴Rt△ADF≌Rt△ABE, 从而△ADF≌△ABF, ∴BF⊥AE, ∴∠DFB为二面角D-AE-B的平面角, 在Rt△ADE中, 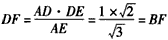 , ,又 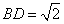 , ,在△DFB中,由余弦定理得 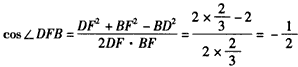 , ,∴ 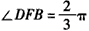 , ,即二面角D-AE-B的大小为 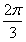 。 。 |
 |

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.